
En el mundo de la investigación de mercados y el análisis de datos, una de las tareas más comunes es entender la relación entre diferentes variables. Queremos saber si la satisfacción del cliente está vinculada a la lealtad, si la percepción de la marca influye en el volumen de compra, o si la clasificación de un focus group sobre varios productos es consistente.Hoy hablaremos de uno de los métodos de correlación no paramétricos, el Coeficiente de correlación de rangos de Kendall, a menudo denominado Tau de Kendall.
Tradicionalmente, el Coeficiente de correlación de Pearson ha sido el estándar de oro. Sin embargo, este método tiene un requisito estricto: asume que las variables siguen una distribución normal y que la relación entre ellas es lineal. ¿Qué pasa cuando trabajamos con datos ordinales (rangos, clasificaciones) o cuando la distribución de los datos es desconocida o marcadamente no normal? Ahí es donde entra el Coeficiente de correlación de rangos de Kendall.
Este coeficiente proporciona una medida robusta y precisa de la concordancia o disparidad entre las clasificaciones asignadas a un conjunto de objetos o individuos por dos observadores o por dos variables diferentes.
En este artículo, exploraremos en detalle qué es el Tau de Kendall, cómo se diferencia de otros métodos como la ρ (Rho) de Spearman, por qué es vital en el análisis de encuestas y rankings.
¿Qué es el coeficiente de correlación de rangos de Kendall (τ)?
El coeficiente de correlación de rangos de Kendall (τ) es una estadística no paramétrica utilizada para medir la fuerza y dirección de la asociación entre dos variables a nivel ordinal. En términos simples, evalúa la similitud en las clasificaciones de un conjunto de datos cuando son clasificadas por dos criterios o evaluadores distintos.
A diferencia del coeficiente de Spearman, que se basa en las distancias de las diferencias de rango, el Tau de Kendall se fundamenta en el concepto de pares concordantes y pares discordantes.
Pares concordantes y discordantes
Para entender τ, imaginemos que tenemos una lista de n objetos clasificados por dos variables, A y B. Al tomar cualquier par de objetos (i y j), este par puede ser:
- Par concordante (C): Si el ranking del objeto i con respecto al objeto j es el mismo tanto en la variable A como en la variable B. Es decir, si A califica a i por encima de j, y B también califica a i por encima de j (o si ambos califican a j por encima de i). La clasificación relativa es la misma.
- Par discordante (D): Si el ranking del objeto i con respecto al objeto j es el opuesto en las variables A y B. Es decir, si A califica a i por encima de j, pero B califica a j por encima de i. La clasificación relativa es diferente.
- Empate: Si los objetos tienen el mismo ranking en A, en B, o en ambas.
El coeficiente τ es esencialmente una proporción que compara la diferencia entre el número de pares concordantes y discordantes con el número total de pares no empatados.
Tipos de coeficiente de correlación de rangos de Kendall
Existen tres variantes principales del coeficiente de correlación de rangos de Kendall, diseñadas para manejar diferentes escenarios de datos:
τa (Tau-a de Kendall)
- Uso: Es la forma original y la más simple. Se utiliza cuando no hay empates en ninguno de los rangos. Es muy raro encontrar datos de encuestas sin ningún empate, por lo que su uso es limitado en la práctica de la investigación de mercados.
- Fórmula (simplificada):
τa=21n(n−1)C−D
Donde n(n−1)/2 es el número total de pares posibles.
τb (Tau-b de Kendall)
- Uso: Es la versión más utilizada en el análisis estadístico real. Está diseñada para manejar la presencia de empates (ties) en las clasificaciones. Ajusta el denominador de la fórmula para tener en cuenta los empates, lo que asegura que el valor de τb pueda alcanzar el rango de [−1,+1].
- Ideal para: El análisis de correlación de ítems de escala Likert, preguntas de clasificación o datos donde es común que varios encuestados asignen la misma puntuación.
τc (Tau-c de Kendall)
- Uso: También maneja empates, pero está específicamente diseñada para utilizarse en tablas de contingencia o cuando las variables no tienen el mismo número de categorías (tablas rectangulares, r×c). A menudo se le llama el coeficiente de correlación para tablas rectangulares.
- Ideal para: Datos donde se cruzan dos variables ordinales con diferente número de niveles.
Para la mayoría de los análisis de encuestas y correlaciones de rangos en investigación de mercados, el τb de Kendall es el coeficiente de elección.
Ventajas del coeficiente de Kendall sobre otros métodos
La elección de un estadístico de correlación no es trivial; debe basarse en la naturaleza de los datos. El Tau de Kendall ofrece beneficios significativos sobre sus contrapartes:
1. Robustez frente a la distribución
A diferencia del ρ de Pearson, el Tau de Kendall no requiere que los datos sigan una distribución normal. Esto es crucial, ya que muchos datos de encuestas (ingreso, tiempo de permanencia, respuestas a escalas Likert) son inherentemente no normales (sesgados).
2. Mayor interpretabilidad
El valor de τ tiene una interpretación probabilística más directa que el ρ de Spearman. τ representa la diferencia entre la probabilidad de que los rangos observados estén en el mismo orden (concordancia) y la probabilidad de que estén en orden diferente (discordancia).
Un τ=0.80 significa que la probabilidad de que dos observadores (o variables) clasifiquen un par de objetos en el mismo orden es 80% mayor que la probabilidad de que los clasifiquen en orden opuesto.
3. Menor sensibilidad a los empates
Mientras que tanto Spearman como Kendall tienen versiones que manejan empates, la versión τb de Kendall tiende a ser más estable y proporcionar una estimación de correlación más precisa cuando hay un gran número de valores empatados en los datos (algo común en escalas Likert de 5 o 7 puntos).
4. Menor sensibilidad a valores extremos
Al basarse únicamente en la ordenación de los datos y no en las diferencias de valores absolutos, el Tau de Kendall es menos afectado por outliers o valores extremos que podrían distorsionar la correlación de Pearson.
| Característica | $\rho$ de Pearson | $\rho$ de Spearman | $\tau$ de Kendall |
|---|---|---|---|
| Tipo de datos | Intervalo o Razón | Ordinal (Rangos) | Ordinal (Rangos) |
| Asunción de distribución | Normal | No se asume | No se asume |
| Sensibilidad a outliers | Alta | Media | Baja |
| Base del cálculo | Valores absolutos | Diferencia de rangos | Pares concordantes/discordantes |
| Rango del coeficiente | $[-1, +1]$ | $[-1, +1]$ | $[-1, +1]$ |
Usos del coeficiente τ de Kendall en la investigación
El coeficiente de Kendall es una herramienta versátil y poderosa, particularmente útil en escenarios donde el orden o la clasificación son las métricas clave.
1. Fiabilidad inter-evaluador
Este es quizás su uso más directo. Cuando múltiples expertos, jueces o encuestados clasifican un mismo conjunto de ítems (p. ej., la calidad de cinco anuncios de televisión, la usabilidad de tres interfaces de software), τ se utiliza para determinar si existe una concordancia significativa entre sus juicios. Un alto τ indica que los evaluadores están de acuerdo en el orden de las clasificaciones.
2. Correlación de variables ordinales en encuestas
En la investigación de experiencia del cliente (CX) y experiencia del empleado (EX), es común usar escalas Likert (p. ej., de 1 a 5, “Totalmente en desacuerdo” a “Totalmente de acuerdo”). Si queremos correlacionar la variable “Satisfacción general” (ordinal) con la variable “Probabilidad de recomendación” (ordinal, escala NPS), el Tau de Kendall es el método estadístico más apropiado.
3. Análisis de preferencias y ranking
Si realizas un estudio de análisis conjoint simplificado o utilizas preguntas de ordenación por rangos (Rank Order), los datos resultantes son puramente ordinales. τ de Kendall te ayuda a correlacionar:
- El ranking de preferencias de un grupo demográfico (A) con el de un grupo demográfico (B).
- El ranking de importancia de características con el ranking de satisfacción de esas mismas características.
4. Detección de tendencias no lineales
Aunque el Tau de Kendall no asume linealidad, es excelente para identificar tendencias monótonas. Esto significa que, si a medida que una variable aumenta, la otra tiende a aumentar (o disminuir), τ lo detectará, incluso si la relación no es una línea recta perfecta.
Cómo se calcula el coeficiente de correlación de Kendall
La belleza del Tau de Kendall radica en su fundamento lógico de pares. Aunque las plataformas modernas como QuestionPro se encargan del cálculo, entender el proceso ayuda a interpretar el resultado. El cálculo del τb (el más usado) implica los siguientes pasos:
Paso 1: ordenar los datos
Selecciona una de las dos variables (digamos, Variable X) y ordena todos los pares de datos basándote en ella, de menor a mayor.
Paso 2: identificar los pares concordantes (C) y discordantes (D)
Para cada par de observaciones (comparando la primera observación con la segunda, la primera con la tercera, etc.), examina la segunda variable (Variable Y) en la lista ordenada.
- Pares concordantes (C): Cuenta cuántas veces el valor de Y en la segunda observación es mayor que el valor de Y en la primera observación.
- Pares discordantes (D): Cuenta cuántas veces el valor de Y en la segunda observación es menor que el valor de Y en la primera observación.
- Empates: Ignora los pares donde el valor de Y es igual (empate).
Paso 3: aplicar la fórmula de τb (ajustada por empates)
El coeficiente de τb se calcula de la siguiente manera:
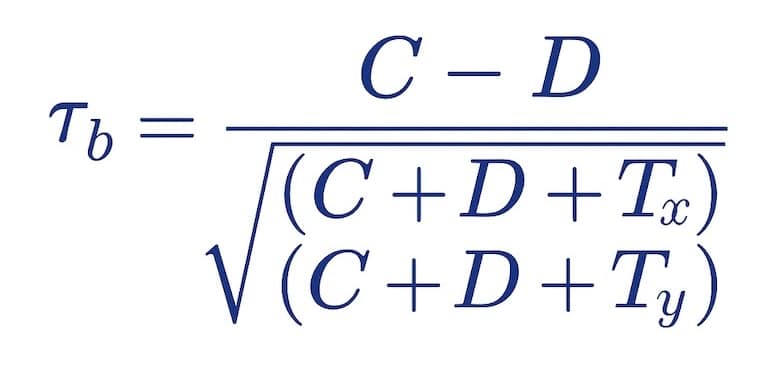
Donde:
- C: Número total de pares concordantes.
- D: Número total de pares discordantes.
- Tx: Número de pares empatados solo en la variable X.
- Ty: Número de pares empatados solo en la variable Y.
Interpretación del resultado
El valor resultante de τ siempre oscilará entre −1 y +1:
- τ=+1: Correlación perfecta positiva. Los rangos de ambas variables son idénticos. Acuerdo total.
- τ=−1: Correlación perfecta negativa. Los rangos son inversos (perfectamente opuestos). Desacuerdo total.
- τ=0: Ausencia de correlación. No hay ninguna relación monótona entre los rangos.

Nota: La interpretación de la fuerza siempre debe ir acompañada del valor p para determinar si la correlación es estadísticamente significativa.
Herramientas para calcular el coeficiente de correlación de rangos de Kendall
Aunque el cálculo manual es útil para la comprensión, en la práctica de la investigación de mercados, se utilizan herramientas de software especializadas para manejar grandes volúmenes de datos.
1. Software estadístico especializado
Programas como SPSS, R o Stata ofrecen módulos completos para el cálculo del τ de Kendall, así como la capacidad de realizar pruebas de hipótesis para determinar la significancia estadística del coeficiente. Son ideales para analistas de datos avanzados.
2. Hojas de cálculo (limitado)
Hojas de cálculo como Excel o Google Sheets no tienen una función nativa para el Tau de Kendall. Se requeriría programar una fórmula compleja o utilizar complementos de terceros, lo cual es ineficiente y propenso a errores para la mayoría de los investigadores.
3. Plataformas de encuestas
La forma más eficiente y accesible para los investigadores de mercado y profesionales de CX/EX es utilizar una plataforma de encuestas que integre estas capacidades analíticas directamente. QuestionPro no solo facilita la recopilación de datos ordinales (con preguntas de Likert, Rank Order, y escalas de matriz), sino que también permite exportar los datos o, mejor aún, utilizar sus herramientas de análisis y segmentación para identificar rápidamente las variables correlacionadas.
Ejemplo de aplicación en experiencia del cliente (CX)
Imaginemos que una empresa ha recopilado datos de una encuesta de satisfacción (Customer Satisfaction, CSAT) después de una interacción de soporte técnico.
Variables medidas (ambas ordinales):
- X: Habilidad del Agente (Clasificación de 1 a 5, siendo 5 “Excelente”)
- Y: Satisfacción General con la Interacción (Clasificación de 1 a 5, siendo 5 “Muy Satisfecho”)
Objetivo: Determinar la fuerza de la relación entre la percepción de la habilidad del agente y la satisfacción general del cliente.
Análisis con Tau de Kendall:
- Resultados hipotéticos: Tras el análisis, el software estadístico arroja un resultado de τb=0.72 con un valor p <0.001.
- Interpretación:
- Fuerza: El valor de 0.72 indica una correlación fuerte y positiva.
- Dirección: Positiva significa que a medida que los clientes clasifican la “Habilidad del Agente” más alto (mayor rango), también clasifican la “Satisfacción General” más alto.
- Significancia: El valor p muy bajo (<0.001) confirma que esta correlación no es producto del azar y es estadísticamente significativa.
- Concordancia: La probabilidad de que un cliente clasifique dos interacciones en el mismo orden de habilidad y satisfacción es significativamente mayor que la probabilidad de que las clasifique en orden inverso.
Acción empresarial (Insight): Este resultado valida la estrategia de inversión en capacitación de agentes. Muestra que la habilidad percibida del personal de soporte es el principal predictor del éxito de la interacción, proporcionando una hoja de ruta clara para mejorar la CX.
Conclusión
El coeficiente de correlación de rangos de Kendall proporciona una manera robusta y estadísticamente correcta de medir la concordancia y la asociación entre datos ordinales, que son el pan de cada día en la investigación de mercados, la evaluación de la experiencia del cliente y los estudios de preferencias.
El poder de τ reside en su capacidad para ofrecer insights limpios y menos sesgados por asunciones de normalidad o por valores extremos. Utilizar τ de Kendall para validar la consistencia en los juicios de tus encuestados, correlacionar tus métricas de CSAT con el NPS, o entender las preferencias de clasificación, te permite tomar decisiones basadas en datos con un alto grado de confianza.
QuestionPro permite:
- Diseñar preguntas ordinales avanzadas: Utiliza preguntas de matriz, clasificación por rangos, y escalas Likert, que son la fuente de los datos para τ de Kendall.
- Recolectar datos limpios y en volumen: Recopila datos de manera eficiente a través de diversos canales.
- Preparar los datos para un análisis avanzado: Con la función de exportación de datos y la integración con herramientas de análisis estadístico, puedes aplicar τ de Kendall a tus conjuntos de datos masivos sin esfuerzo.
Entender la concordancia entre las percepciones de tus clientes es el primer paso para optimizar sus experiencias. No dejes tus insights más valiosos al azar o a métodos inadecuados.
Descubre la verdadera fuerza de tus datos ordinales. Crea tu cuenta gratuita en QuestionPro hoy mismo y comienza a diseñar encuestas que te proporcionen los insights que necesitas para tomar decisiones estratégicas basadas en la concordancia de tus clientes.



