
¿Alguna vez te has preguntado qué tan estrechamente relacionadas están dos cosas, como si más horas de estudio significan mejores calificaciones o si más dinero implica más gastos? Un análisis del coeficiente de correlación puede ayudarte a averiguarlo y a tomar decisiones informadas. Es una forma numérica de medir la fuerza y la dirección de la relación entre dos cosas.
Un coeficiente de correlación varía de -1 a +1, por lo que es una poderosa herramienta estadística para ver cómo interactúan las cosas. Comprender esto es clave para el análisis de datos en muchos campos.
En este artículo, exploraremos los coeficientes de correlación, sus fórmulas y ejemplos del mundo real. Ya seas estudiante, investigador o entusiasta de los datos, adquirirás el conocimiento para aplicar el análisis de correlación de manera efectiva en tu trabajo.
¿Qué es el coeficiente de correlación?
Un coeficiente de correlación es una estadística descriptiva que mide la relación entre dos variables. Es una medida tangible de la asociación.
Esto es importante para comprender el significado práctico de los datos. Te dice qué tan fuerte y en qué dirección están relacionadas dos variables. Los coeficientes de correlación resumen la fuerza y la dirección de una relación lineal, proporcionando una imagen clara de la interacción entre variables.
El valor del coeficiente de correlación varía de -1 a 1:
- -1 es una correlación negativa perfecta.
- 1 es una correlación positiva perfecta.
- 0 es ninguna correlación en absoluto, correlación nula.
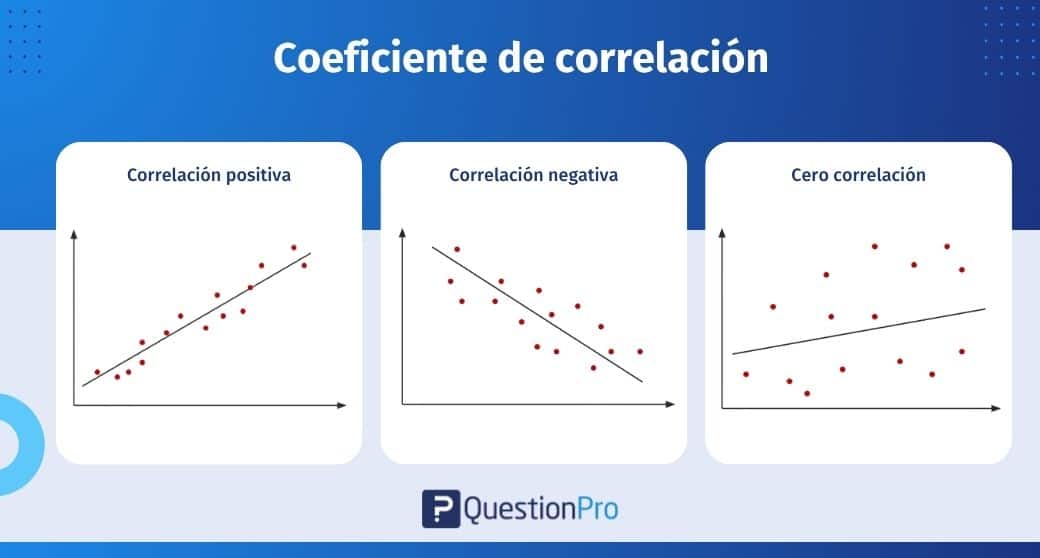
Un valor absoluto mayor del coeficiente de correlación significa una relación más fuerte entre las variables. Por ejemplo, un coeficiente de correlación cercano a 1 significa una relación positiva fuerte, y un valor cercano a -1 significa una relación negativa fuerte.
Una de las mejores cosas de los coeficientes de correlación es que no tienen unidades, por lo que puedes comparar entre diferentes conjuntos de datos. Desde las finanzas hasta los estudios ambientales, esto los hace súper útiles en muchos campos, donde comprender la relación lineal entre variables puede ser realmente revelador.
Interpretación de los valores del coeficiente de correlación
Interpretar los valores de los coeficientes de correlación es clave para comprender las relaciones entre variables. +1 significa una relación positiva perfecta donde las variables se mueven en la misma dirección. -1 significa una relación negativa perfecta donde una variable aumenta mientras la otra disminuye.
Estos valores extremos son raros, pero representan la relación más fuerte posible entre dos variables.
Una correlación positiva significa que una variable aumenta a medida que la otra también tiende a aumentar. Por ejemplo, 0.8 a menudo se interpreta como una correlación positiva fuerte, donde las variables se mueven juntas en una dirección similar. Por otro lado, negativa significa que una aumenta a medida que la otra disminuye. Esto está representado por valores negativos del coeficiente de correlación, donde las variables están inversamente relacionadas.
Valores cercanos a cero significan ninguna correlación o relación lineal entre las variables. Por ejemplo, un coeficiente de correlación de 0.2 a 0.4 significa una correlación débil, solo una ligera asociación entre variables. Los valores atípicos (outliers) pueden afectar los coeficientes de correlación y distorsionar la relación. Por lo tanto, considera siempre el contexto de los datos y las posibles anomalías al interpretar los valores de correlación.
Los ejemplos prácticos ayudarán a ilustrar esto. 0.5298 significa una correlación positiva moderada, una relación visible pero no fuerte entre variables. Comprender estos matices te ayudará a analizar mejor los datos y a tomar mejores decisiones en muchos campos.
Tipos de coeficientes de correlación
Los coeficientes de correlación vienen en varias formas, cada una adecuada para diferentes tipos de datos y relaciones. Los coeficientes de correlación más utilizados incluyen la r de Pearson, la rho (ρ) de Spearman y la tau (τ) de Kendall, cada uno sirviendo a necesidades analíticas específicas. Estos coeficientes pueden variar según el tipo de relación, los niveles de medición y la distribución de los datos.
El coeficiente de correlación de Pearson es el tipo más popular y se utiliza ampliamente para medir relaciones lineales y correlación lineal entre dos variables cuantitativas. Es particularmente efectivo cuando los datos cumplen con ciertos supuestos, como la distribución normal y la linealidad.
Por otro lado, la ρ de Spearman es una alternativa no paramétrica a la r de Pearson. Es adecuada para datos ordinales o no distribuidos normalmente. Esto la convierte en una herramienta versátil para analizar variables ordenadas por rango.
Otros tipos de coeficientes de correlación incluyen:
- Correlación punto biserial: se utiliza cuando una variable es dicotómica y la otra es cuantitativa.
- V de Cramér: es aplicable para medir la correlación entre dos variables nominales.
- Tau de Kendall: es otra opción no paramétrica. A menudo se prefiere para tamaños de muestra más pequeños debido a su robustez.
Comprender estos diferentes tipos permite un análisis de datos más adaptado y preciso.
Coeficiente de correlación de Pearson (r)
El coeficiente de correlación de Pearson es la base de la estadística. Describe la relación lineal entre dos variables continuas. Este coeficiente mide la fuerza y dirección de la relación y te da una visión completa de cómo interactúan las variables.
La r de Pearson varía de -1 a 1 y mide cuán linealmente relacionadas están las variables. El coeficiente de correlación poblacional te da una imagen más amplia de estas relaciones.
Se deben cumplir varios supuestos para usar la correlación de Pearson. Estos son:
- Cada punto de datos debe ser independiente de los demás.
- Ambas variables deben medirse en una escala de intervalo o razón.
- La relación entre las dos variables debe ser lineal.
- La dispersión de los residuales debe ser consistente en todo el rango de valores.
- Ambas variables deben seguir distribuciones normales.
- Tus datos no tienen valores atípicos.
- Los datos deben provenir de una muestra aleatoria o representativa.
Además, las variables deben estar distribuidas normalmente y libres de valores atípicos, ya que estos pueden sesgar los resultados. Ambas variables deben ser continuas para que se aplique la correlación de Pearson.
El valor del coeficiente de correlación producto-momento de Pearson varía desde +1, lo que indica una correlación positiva perfecta. -1 indica una correlación negativa perfecta, y 0 significa ninguna correlación. Esta relación es simétrica, por lo que el orden de las variables no importa.
Además, el coeficiente no tiene unidades para que puedas comparar a través de diferentes escalas. Por lo tanto, la r de Pearson es una buena medida estadística para una relación lineal entre dos variables continuas.
Cálculo del coeficiente de correlación de Pearson
Calcular el coeficiente de correlación de Pearson es un proceso simple pero preciso. La fórmula del coeficiente de correlación encuentra la relación entre las variables. Devuelve valores entre -1 y 1. Utiliza la calculadora del coeficiente de correlación de Pearson a continuación para ver qué tan fuertes son las dos variables.
La fórmula para el coeficiente de correlación r de Pearson es:
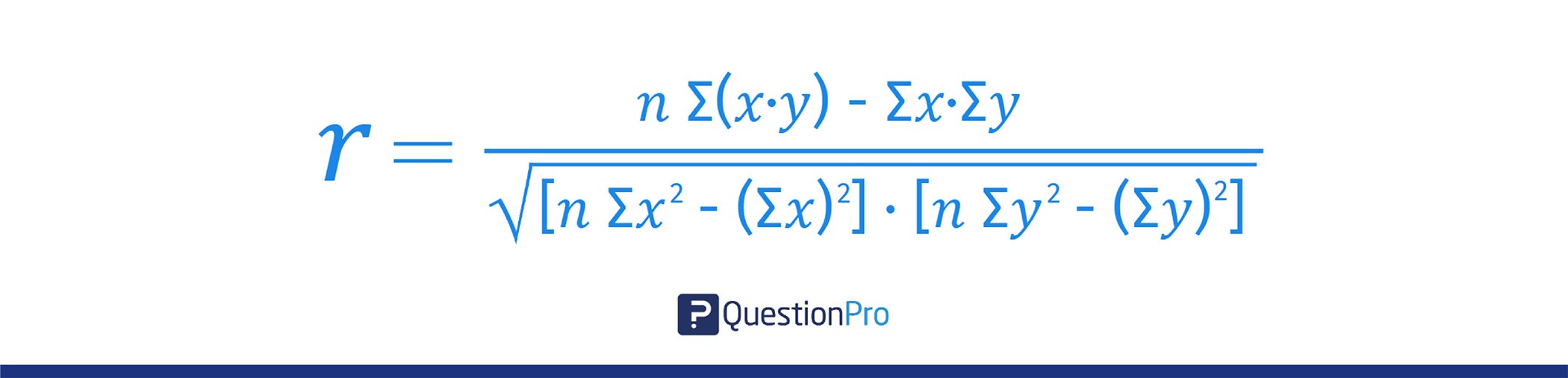
Donde:
- n: número de pares de datos.
- ∑x: suma de los valores x.
- ∑y: suma de los valores y.
- ∑(x⋅y): suma del producto de los valores x e y emparejados.
- ∑x2: suma de los valores x al cuadrado.
- ∑y2: suma de los valores y al cuadrado.
Usemos un ejemplo para calcular la correlación entre edad e ingresos. Organiza tus datos en una tabla con ambas variables.
| Persona | Edad (𝑥) | Ingresos (𝑦) |
| 1 | 20 | 1500 |
| 2 | 25 | 2500 |
| 3 | 30 | 3000 |
| 4 | 40 | 5000 |
| 5 | 50 | 7500 |
Añade tres columnas adicionales para:
- 𝑥⋅𝑦: El producto de los valores correspondientes de 𝑥 y 𝑦.
- 𝑥2: El cuadrado de cada valor de 𝑥.
- 𝑦2: El cuadrado de cada valor de 𝑦.
Calcula y rellena los valores de 𝑥⋅𝑦, 𝑥2 y 𝑦2 para cada fila. A continuación, suma cada columna para obtener los totales de ∑𝑥, ∑𝑦, ∑(𝑥⋅𝑦), ∑𝑥2 y ∑𝑦2.
| Persona | Edad (𝑥) | Ingresos (𝑦) | 𝑥⋅𝑦 | 𝑥² | 𝑦² |
| 1 | 20 | 1500 | 30000 | 400 | 2250000 |
| 2 | 25 | 2500 | 625000 | 625 | 6250000 |
| 3 | 30 | 3000 | 90000 | 900 | 9000000 |
| 4 | 40 | 5000 | 200000 | 1600 | 25000000 |
| 5 | 50 | 7500 | 375000 | 2500 | 56250000 |
| Total | 165 | 19500 | 757500 | 6025 | 99000000 |
Llena los valores de la tabla:
- 𝑛 = 5
- ∑𝑥 = 165
- ∑𝑦 = 19500
- ∑(𝑥⋅𝑦) = 757500
- ∑𝑥2 = 6025
- ∑𝑦2 = 99000000
Sustituye estos valores en la fórmula y calcula 𝑟. Si el resultado es:
- Cerca de +1: fuerte relación lineal positiva.
- Cerca de -1: fuerte relación lineal negativa.
- Cerca de 0: relación lineal débil o inexistente.
El coeficiente de correlación de Pearson (𝑟) de los datos proporcionados es aproximadamente 0,988. Dado que 𝑟 es muy cercano a +1, existe una fuerte relación lineal positiva entre las dos variables (edad e ingresos). Esto significa que, a medida que aumenta la edad, los ingresos aumentan linealmente.
Así pues, aquí vemos lo importante que es comprender los datos y calcularlos correctamente. Siguiendo estos pasos, puede obtener información valiosa de sus datos y tomar decisiones basadas en la fuerza y la dirección de las relaciones lineales.
También puede utilizar Excel para calcular fácilmente los coeficientes de correlación. Todo lo que tiene que hacer es introducir sus datos en dos columnas y seleccionar una celda para colocar el resultado. Para obtener el coeficiente de correlación de Pearson en Excel, utilice la fórmula =CORREL(rango1, rango2) y seleccione los rangos de datos correctos.
Coeficiente de correlación de rangos de Spearman
La correlación de rangos de Spearman es una alternativa no paramétrica a la correlación de Pearson. Es útil cuando tus datos no cumplen las suposiciones de r de Pearson. Este coeficiente clasifica los puntos de datos de cada variable y mide las diferencias entre esas clasificaciones. Prueba qué tan bien se pueden modelar dos variables mediante una función monotónica, no lineal.
Para comprender el coeficiente de correlación de Spearman, necesitas saber qué es una función monotónica. Una función monotónica es aquella que nunca disminuye o nunca aumenta a medida que aumenta la variable ‘x’. Una función monotónica se puede explicar usando la siguiente imagen:
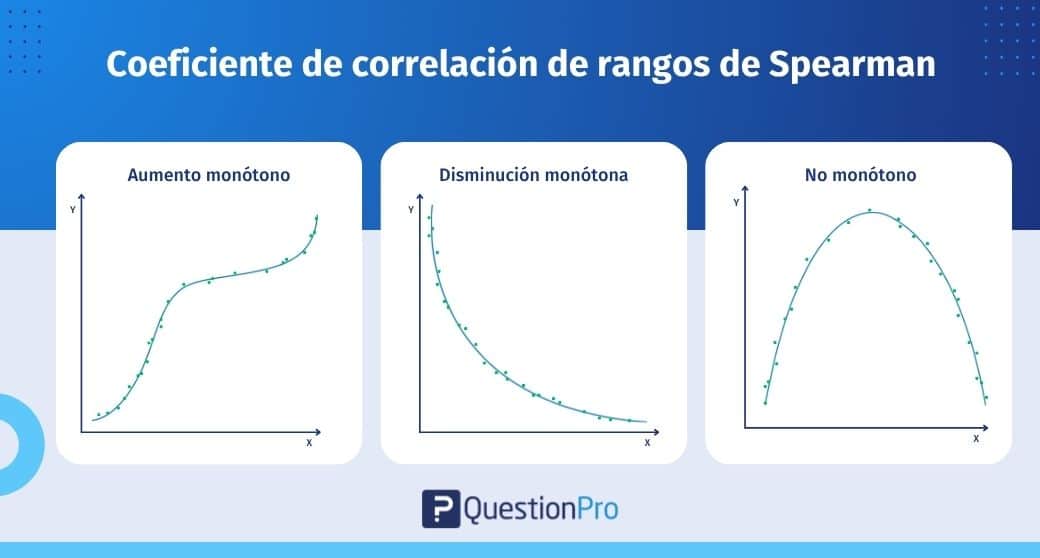
La imagen explica tres tipos de funciones monotónicas:
- Monotónicamente creciente: Cuando ‘x’ aumenta e ‘y’ nunca disminuye.
- Monotónicamente decreciente: Cuando ‘x’ aumenta pero ‘y’ nunca aumenta.
- No monotónica: Cuando ‘x’ aumenta e ‘y’ a veces aumenta y a veces disminuye.
Una relación monotónica es menos restrictiva que una relación lineal, como la utilizada en el coeficiente de Pearson. Aunque la monotonicidad no es un requisito para el coeficiente de correlación de Spearman, no tendrá sentido buscar la correlación de Spearman si ya sabes que la relación entre las variables no es monotónica.
El uso de la correlación de rangos de Spearman ayuda a los analistas a obtener información sobre la fuerza y la dirección de las relaciones en varios escenarios de datos, mejorando su capacidad para interpretar los hallazgos.
Cálculo del coeficiente de correlación de rangos de Spearman
Los símbolos para el rho de Spearman son ρ para el coeficiente de población y rs para el coeficiente de correlación de la muestra. La fórmula para el coeficiente de correlación de rangos de Spearman es:
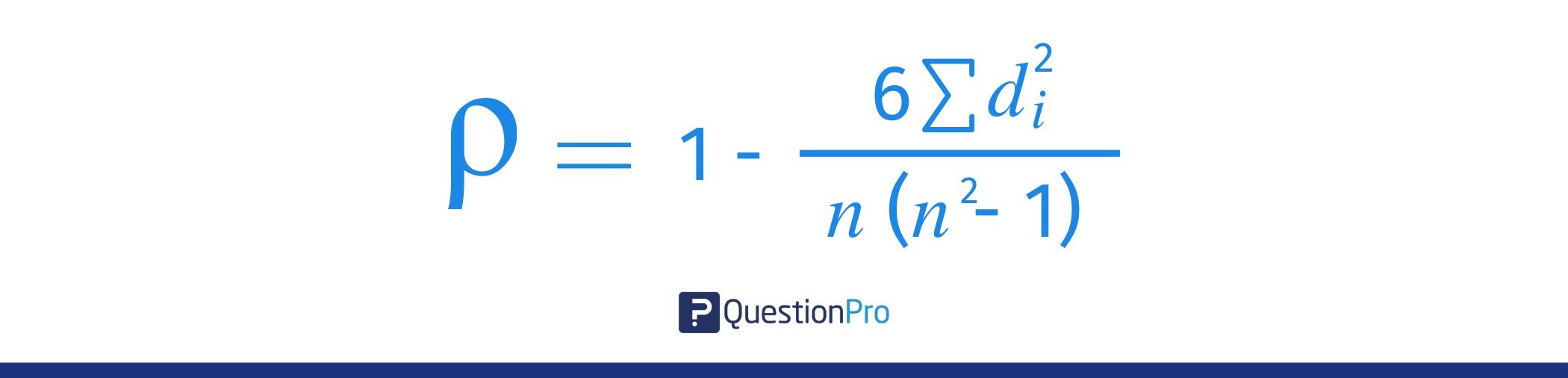
Donde:
- di: La diferencia entre los rangos de cada par de observaciones (di=R(xi)−R(yi)
- n: El número de observaciones
- ∑di2: La suma de las diferencias al cuadrado entre los rangos
Para usar esta fórmula, encontrarás las diferencias (di) entre los rangos de tus variables para cada par de datos y tomarás eso como la entrada principal para la fórmula.
El coeficiente de correlación de rangos de Spearman ρ puede tomar un valor entre +1 y −1 donde:
- ρ de 1 significa que todas las clasificaciones para cada variable coinciden perfectamente.
- ρ de −1 significa que las clasificaciones están en el orden exactamente opuesto.
- ρ de 0 significa que no hay relación monotónica, y las variables no tienen una dirección consistente.
Es por eso que el rho de Spearman es excelente para datos ordinales o conjuntos de datos con valores atípicos, ya que puede mostrar una correlación cero.
Usemos un ejemplo para calcular el coeficiente de correlación de rangos de Spearman. Tenemos las puntuaciones de 9 estudiantes en Historia y Geografía de la siguiente manera:
| Historia | Geografíay |
| 35 | 30 |
| 23 | 33 |
| 47 | 45 |
| 17 | 23 |
| 10 | 8 |
| 43 | 49 |
| 9 | 12 |
| 6 | 4 |
| 28 | 31 |
Comienza por clasificar las puntuaciones tanto de Historia como de Geografía. Asigna el rango “1” a la puntuación más alta, “2” a la segunda más alta, y así sucesivamente. Si dos valores son iguales, asígnales la media de los rangos que ocuparían si fueran distintos.
| Historia | Rango | Geografía | Rango |
| 35 | 3 | 30 | 5 |
| 23 | 5 | 33 | 3 |
| 47 | 1 | 45 | 2 |
| 17 | 6 | 23 | 6 |
| 10 | 7 | 8 | 8 |
| 43 | 2 | 49 | 1 |
| 9 | 8 | 12 | 7 |
| 6 | 9 | 4 | 9 |
| 28 | 4 | 31 | 4 |
| Historia | Rango | Geografía | Rango | 𝑑 | 𝑑2 |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
Ahora, suma todas las diferencias al cuadrado (𝑑2):
- ∑d2=4+4+1+0+1+1+1+0+0=12
- También, n=9
Entonces, el coeficiente de correlación de rangos de Spearman es:
𝑟𝑠 = 1 – { 6 ∑𝑑𝑖2 / 𝑛 ( 𝑛2-1 ) }
= 1 – { ( 612 ) / ( 9( 81-1 ) }
= 1 – {72 / 720}
= 1 – 0.1
= 0.9
El coeficiente de correlación de rangos de Spearman es rs=0.9, lo que significa que hay una fuerte correlación positiva entre las puntuaciones de Historia y Geografía. Por lo tanto, los estudiantes a los que les va bien en Historia también tienden a obtener buenos resultados en Geografía.
Usos de los coeficientes de correlación
Los coeficientes de correlación se utilizan en muchas aplicaciones de la vida real para tomar decisiones en múltiples campos. Aquí tienes algunas de ellas:
Finanzas
En finanzas, los coeficientes de correlación ayudan a evaluar el riesgo y diversificar una cartera al analizar la relación entre diferentes valores. Los traders cuantitativos también utilizan estos coeficientes para pronosticar cambios a corto plazo en los precios de los valores y así mejorar sus estrategias de trading.
Investigación ambiental
Los estudios ambientales se benefician mucho del análisis de correlación. Por ejemplo, una matriz de coeficientes de correlación puede mostrar las correlaciones significativas entre los elementos traza. Los coeficientes de correlación altos de elementos traza en el río Gomati muestran fuentes geogénicas comunes, y el aluminio tiene la correlación más alta con Fe, Ni, Ti y Rb. Estos conocimientos son importantes para comprender los patrones ambientales y las fuentes de contaminación.
Estudios genéticos
La investigación genética también utiliza coeficientes de correlación para analizar las relaciones dentro de las variaciones genéticas. Por ejemplo, se observaron coeficientes de correlación de Pearson de 0.783 a 0.895 al estudiar las diferencias genéticas en las poblaciones de arroz silvestre. Estos análisis ayudan a comprender la diversidad genética y las tendencias evolutivas.
Limitaciones del análisis de correlación
Si bien el análisis de correlación proporciona información valiosa, tiene ciertas limitaciones. Una de las cosas más importantes que debes recordar es que la correlación no implica causalidad. Factores externos, como las variables de confusión, pueden tergiversar la correlación entre dos variables y conducir a conclusiones erróneas. Por ejemplo, una tercera variable, como el clima cálido, podría influir en la correlación entre las ventas de helados y los incidentes de ahogamiento.
El rango de observaciones también puede afectar los coeficientes de correlación. Reducir el rango de datos puede cambiar el valor de la correlación y, a veces, ocultar la verdadera relación entre las variables. Los valores atípicos son otro gran problema, ya que pueden sesgar el coeficiente de correlación de Pearson y llevar a interpretaciones erróneas. Por lo tanto, siempre examina los datos y considera los valores atípicos antes de sacar conclusiones del análisis de correlación.
Además, el análisis de correlación es solo para datos bivariados, por lo que no puede evaluar relaciones más allá de dos variables. Esto significa que las relaciones más complejas que involucran múltiples variables necesitan diferentes enfoques analíticos, como el análisis de regresión o el análisis multivariado. Por último, los errores de medición pueden afectar la fiabilidad de los coeficientes de correlación y pueden inflar o desinflar los valores observados.
Cómo realizar un coeficiente de correlación con QuestionPro
Usando la herramienta de correlación de QuestionPro, puedes ver fácilmente las relaciones entre las variables de la encuesta. La matriz y la codificación de colores te ayudarán a ver las correlaciones positivas y negativas y a dar sentido a los datos de tu encuesta.
Para comenzar a analizar las correlaciones en los datos de tu encuesta:
- Inicia sesión en QuestionPro.
- Ve a Mis encuestas desde el panel de control.
- Selecciona la encuesta que deseas analizar.
- Ve a Análisis y haz clic en Análisis de correlación en el menú desplegable.
Cuando abras la herramienta de análisis de correlación, se mostrará una matriz de 2×2. Esta matriz muestra el coeficiente de correlación para las primeras dos preguntas de tu encuesta. La matriz te ayuda a ver la relación entre estas variables.
Si deseas correlacionar otras preguntas o toda la encuesta:
- Selecciona las preguntas que deseas correlacionar en las secciones Filas y Columnas.
- Para ver todas las preguntas, selecciona todas en las Filas y Columnas.
- Haz clic en Recalcular coeficiente de correlación para obtener un nuevo informe de correlación.
La matriz de correlación utiliza una codificación de colores basada en umbrales para que la fuerza de las relaciones sea más fácil de interpretar.
Correlación directa (positiva)
- Verde claro: Coeficientes de correlación entre 0.65 y 0.80, lo que indica una relación positiva de fuerza baja.
- Verde medio: Coeficientes entre 0.80 y 0.90, lo que indica una relación positiva de fuerza moderada.
- Verde oscuro: Coeficientes superiores a 0.90, lo que indica una relación positiva de fuerza alta.
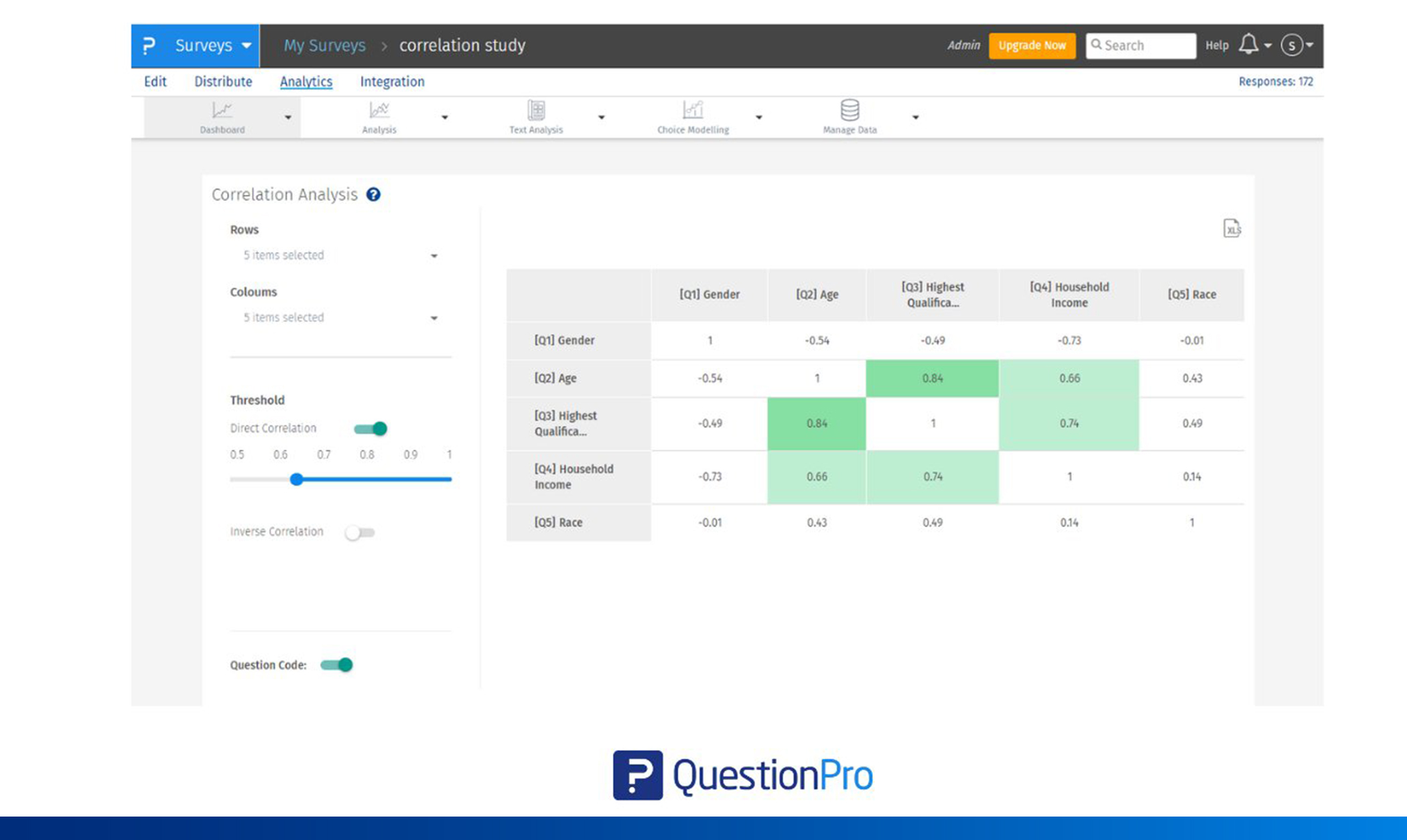
Esto implica que existe una asociación muy fuerte entre las variables. Cualquier aumento en una variable conduce a un aumento en la otra.
Cuando el usuario habilita la correlación inversa, las celdas con relación inversa se resaltan. Tenemos cubos similares en la correlación inversa:
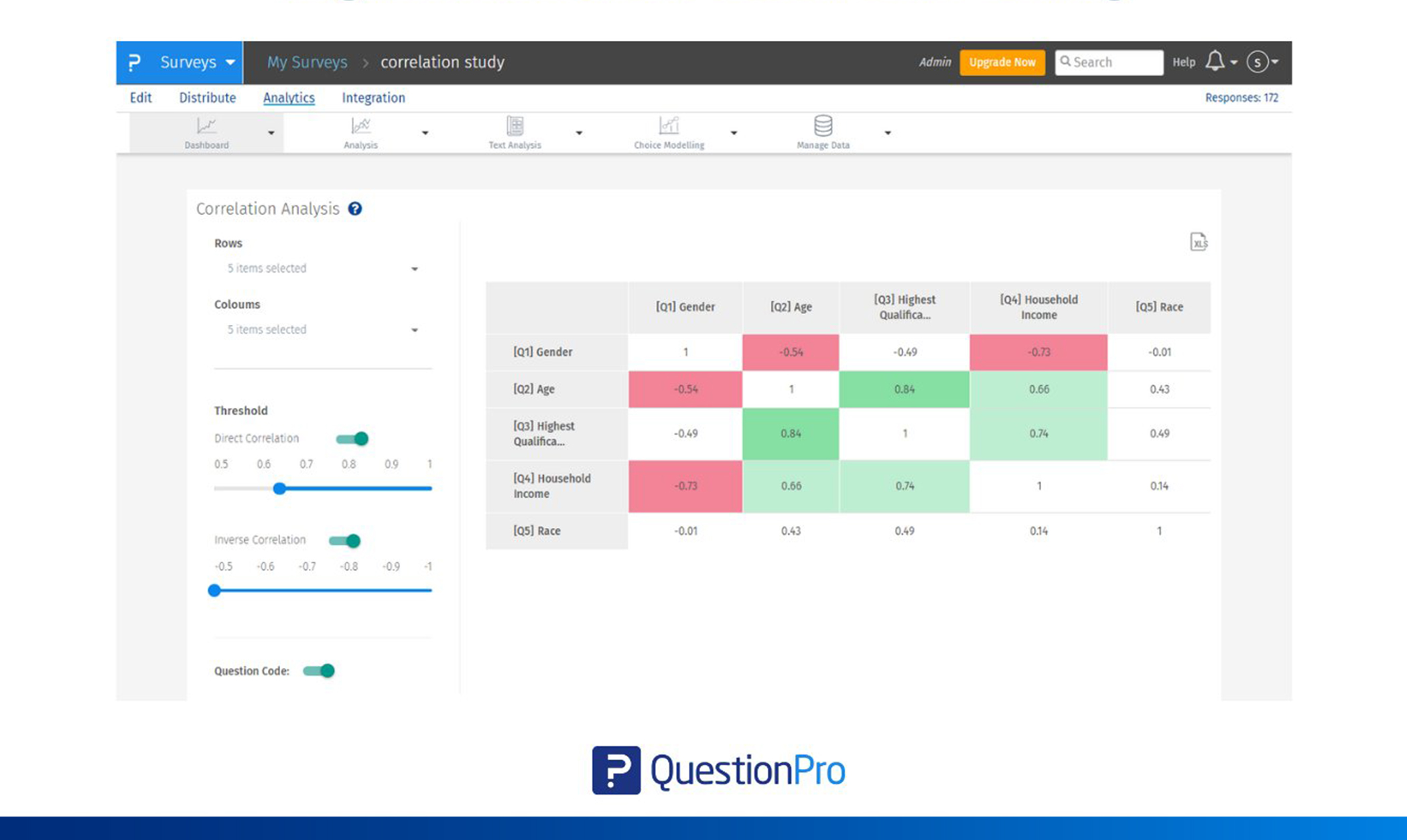
- Rojo claro: Coeficientes de correlación entre −0.65 y −0.80, lo que indica una relación negativa de fuerza baja.
- Rojo medio: Coeficientes entre −0.80 y −0.90, lo que indica una relación negativa de fuerza moderada.
- Rojo oscuro: Coeficientes inferiores a −0.90, lo que indica una relación negativa de fuerza alta.
Conclusión
Los coeficientes de correlación son clave para comprender las relaciones entre variables. Hemos cubierto los conceptos básicos del análisis de correlación, desde la definición del coeficiente de correlación hasta la interpretación de los valores y los diferentes tipos como el de Pearson y el de Spearman. El cálculo de estos coeficientes de forma manual o utilizando herramientas como Excel es una aplicación práctica en diferentes tipos de investigación.
Si bien el análisis de correlación es valioso, tiene sus limitaciones. Al comprender estos conceptos, puedes desbloquear tus datos, tomar decisiones informadas y encontrar patrones significativos. Los coeficientes de correlación son poderosos y puedes usarlos para subir de nivel tus habilidades de análisis de datos.
QuestionPro facilita el análisis de correlación de los datos de encuestas. La interfaz tiene una matriz de correlación con codificación de colores basada en umbrales incorporada, para que puedas ver la fuerza y dirección de las relaciones entre variables. Puedes seleccionar preguntas específicas o todas las preguntas. La plataforma también admite correlaciones inversas, para que puedas ver tanto las relaciones positivas como las negativas.
Ya sea que estés analizando retroalimentación de clientes o datos de investigación académica, la herramienta de análisis de correlación de QuestionPro es una forma poderosa de encontrar patrones y relaciones y tomar decisiones basadas en datos.
Preguntas Frecuentes (FAQs)
Respuesta: 𝑟 es el coeficiente de correlación, que muestra la fuerza y dirección de la relación entre las variables, mientras que 𝑟², o el coeficiente de determinación, indica qué tan bien el modelo explica la varianza en los datos.
Respuesta: Un valor de 0.8 indica una relación positiva bastante fuerte entre dos variables, por lo que, a medida que una variable aumenta, la otra tiende a aumentar también. Esto se considera una relación significativa en los datos.
Respuesta: La principal diferencia entre las correlaciones de Pearson y Spearman es que Pearson mide relaciones lineales en datos cuantitativos, mientras que Spearman mide relaciones monótonas en datos ordenados y es aplicable a datos ordinales o no normales.
Respuesta: Los valores atípicos pueden distorsionar gravemente los coeficientes de correlación, como el de Pearson, y generar resultados engañosos sobre la relación entre las variables. Es necesario identificar y tratar los outliers durante el análisis de correlación.
Respuesta: La correlación puede mostrar la relación entre variables, pero no se puede usar para hacer predicciones sin valores significativos y una línea clara en los datos. Por lo tanto, se debe tener precaución al usar la correlación con fines predictivos.



