Haben Sie sich jemals gefragt, wie eng zwei Dinge miteinander zusammenhängen, z.B. ob mehr Lernstunden zu besseren Noten führen oder mehr Geld zu mehr Ausgaben? Eine Analyse des Korrelationskoeffizienten kann Ihnen helfen, dies herauszufinden und fundierte Entscheidungen zu treffen. Es ist eine numerische Methode, um die Stärke und Richtung der Beziehung zwischen zwei Dingen zu messen.
Ein Korrelationskoeffizient reicht von -1 bis +1 und ist somit ein leistungsfähiges statistisches Werkzeug, um zu sehen, wie Dinge zusammenhängen. Dies zu verstehen ist der Schlüssel zur Datenanalyse in vielen Bereichen.
In diesem Beitrag werden wir uns mit Korrelationskoeffizienten, ihren Formeln und Beispielen aus der Praxis beschäftigen. Egal, ob Sie Student, Forscher oder Datenliebhaber sind, Sie werden das Wissen erlangen, um die Korrelationsanalyse bei Ihrer Arbeit effektiv anzuwenden.
Was ist der Korrelationskoeffizient?
Ein Korrelationskoeffizient ist eine deskriptive Statistik, die die Beziehung zwischen zwei Variablen misst. Er ist ein greifbares Maß für den Zusammenhang.
Dies ist wichtig, um die praktische Bedeutung der Daten zu verstehen. Er sagt Ihnen, wie stark und in welche Richtung zwei Variablen miteinander verbunden sind. Korrelationskoeffizienten fassen die Stärke und Richtung einer linearen Beziehung zusammen und vermitteln ein klares Bild der Interaktion zwischen Variablen.
Der Wert des Korrelationskoeffizienten reicht von -1 bis 1:
- -1 ist eine perfekte negative Korrelation.
- 1 ist eine perfekte positive Korrelation.
- 0 ist überhaupt keine Korrelation.
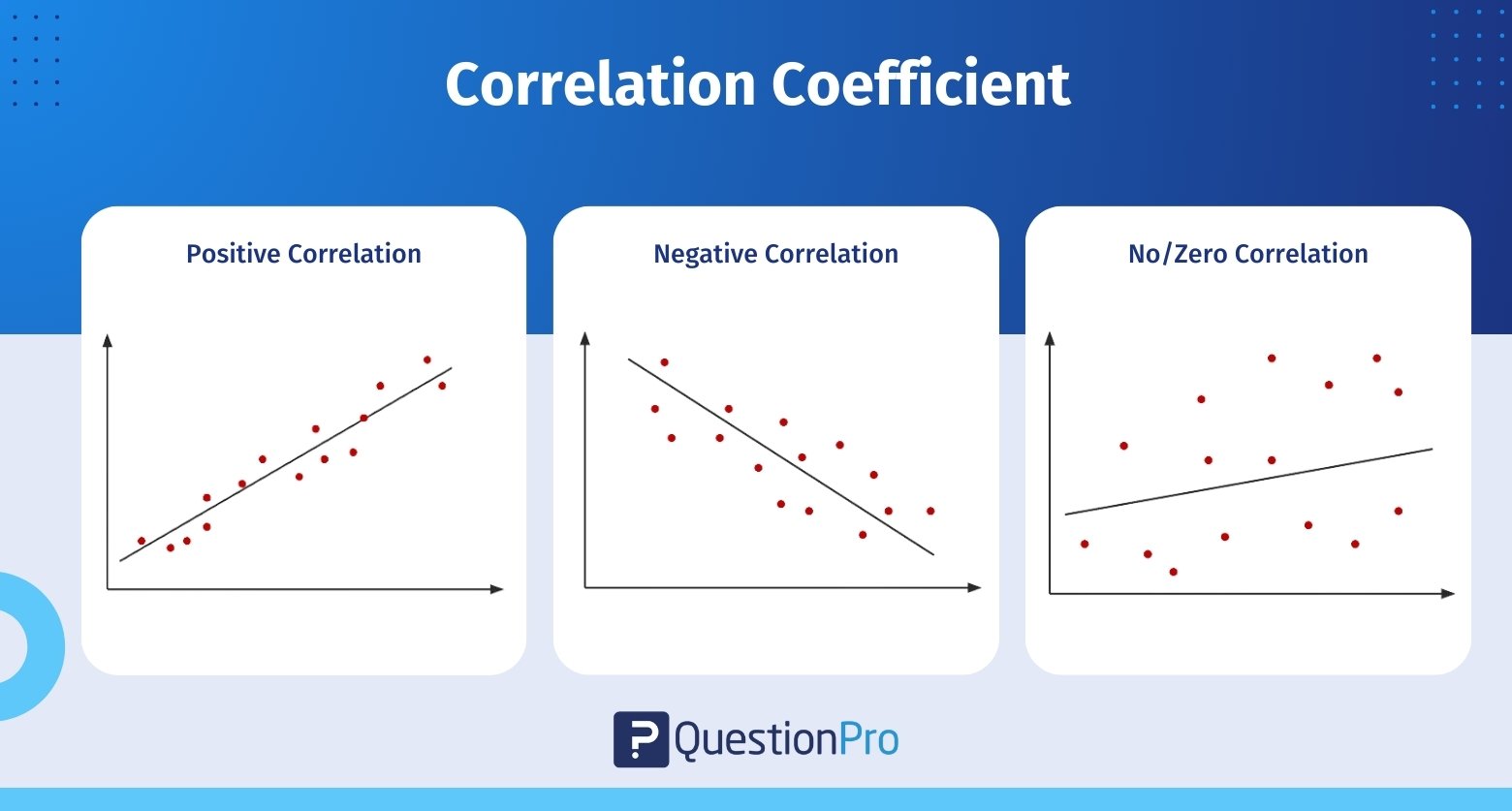
Ein größerer absoluter Wert des Korrelationskoeffizienten bedeutet eine stärkere Beziehung zwischen den Variablen. Zum Beispiel bedeutet ein Korrelationskoeffizient nahe 1 eine starke positive Beziehung und ein Wert nahe -1 eine starke negative Beziehung.
Eines der besten Dinge an Korrelationskoeffizienten ist, dass sie keine Einheiten enthalten, so dass Sie verschiedene Datensätze miteinander vergleichen können. Das macht sie in vielen Bereichen – von der Finanzwirtschaft bis hin zu Umweltstudien – sehr nützlich, da das Verständnis der linearen Beziehung zwischen Variablen sehr aufschlussreich sein kann.
Interpretation der Werte des Korrelationskoeffizienten
Die Interpretation der Werte von Korrelationskoeffizienten ist der Schlüssel zum Verständnis der Beziehungen zwischen Variablen. +1 bedeutet eine perfekte positive Beziehung, bei der sich die Variablen in dieselbe Richtung bewegen. -1 bedeutet eine perfekte negative Beziehung, bei der eine Variable zunimmt, während die andere abnimmt.
Diese Extremwerte sind selten, stellen aber die stärkstmögliche Beziehung zwischen zwei Variablen dar.
Eine positive Korrelation bedeutet, dass eine Variable zunimmt, wenn die andere tendenziell ebenfalls zunimmt. Ein Wert von 0,8 wird zum Beispiel oft als starke positive Korrelation interpretiert, bei der sich die Variablen in eine ähnliche Richtung bewegen. Eine negative Korrelation bedeutet hingegen, dass eine Variable zunimmt, während die andere abnimmt. Dies wird durch negative Werte des Korrelationskoeffizienten dargestellt, wenn die Variablen in umgekehrter Beziehung zueinander stehen.
Werte nahe Null bedeuten keine Korrelation oder lineare Beziehung zwischen den Variablen. Ein Korrelationskoeffizient von 0,2 bis 0,4 bedeutet beispielsweise eine schwache Korrelation, d.h. nur eine geringe Verbindung zwischen den Variablen. Ausreißer können die Korrelationskoeffizienten beeinflussen und die Beziehung verzerren. Berücksichtigen Sie also bei der Interpretation von Korrelationswerten immer den Datenkontext und mögliche Anomalien.
Praktische Beispiele werden dies veranschaulichen. 0,5298 bedeutet eine mäßige positive Korrelation, eine sichtbare, aber nicht starke Beziehung zwischen den Variablen. Das Verständnis dieser Nuancen wird Ihnen helfen, Daten besser zu analysieren und bessere Entscheidungen in vielen Bereichen zu treffen.
Arten von Korrelationskoeffizienten
Korrelationskoeffizienten gibt es in verschiedenen Formen, die jeweils für unterschiedliche Arten von Daten und Beziehungen geeignet sind. Zu den am häufigsten verwendeten Korrelationskoeffizienten gehören Pearson’s 𝑟, Spearman’s rho (ρ) und Kendall’s tau (τ), die jeweils spezifische analytische Anforderungen erfüllen. Diese Koeffizienten können je nach Art der Beziehung, der Messebenen und der Datenverteilung variieren.
Der Korrelationskoeffizient von Pearson ist der beliebteste Typ und wird häufig zur Messung linearer Beziehungen und linearer Korrelationen zwischen zwei quantitativen Variablen verwendet. Er ist besonders effektiv, wenn die Daten bestimmte Annahmen erfüllen, wie z.B. Normalverteilung und Linearität.
Auf der anderen Seite ist Spearmans ρ eine nicht-parametrische Alternative zu Pearsons 𝑟. Sie eignet sich für ordinale oder nicht-normal verteilte Daten. Dies macht sie zu einem vielseitigen Werkzeug für die Analyse von Rangordnungsvariablen.
Andere Arten von Korrelationskoeffizienten sind:
- Punkt-Biserial-Korrelation: Sie wird verwendet, wenn eine Variable dichotom und die andere quantitativ ist.
- Cramér’s V: Dies ist für die Messung der Korrelation zwischen zwei nominalen Variablen geeignet.
- Kendall’s Tau: Dies ist eine weitere nicht-parametrische Option. Sie wird aufgrund ihrer Robustheit oft für kleinere Stichprobengrößen bevorzugt.
Das Verständnis dieser verschiedenen Arten ermöglicht eine maßgeschneiderte und genaue Datenanalyse.
Pearsonscher Korrelationskoeffizient (𝑟)
Der Korrelationskoeffizient von Pearson ist die Grundlage der Statistik. Er beschreibt die lineare Beziehung zwischen zwei kontinuierlichen Variablen. Dieser Koeffizient misst die Stärke und Richtung der Beziehung und gibt Ihnen einen vollständigen Überblick darüber, wie die Variablen zusammenhängen.
Der Pearsonsche 𝑟 reicht von -1 bis 1 und misst, wie linear die Variablen miteinander verbunden sind. Der Korrelationskoeffizient der Bevölkerung gibt Ihnen ein umfassenderes Bild dieser Beziehungen.
Um die Pearson-Korrelation zu verwenden, müssen mehrere Annahmen erfüllt sein. Diese sind:
- Jeder Datenpunkt muss unabhängig von den anderen sein.
- Beide Variablen sollten auf einer Intervall- oder Verhältnisskala gemessen werden.
- Die Beziehung zwischen den beiden Variablen sollte linear sein.
- Die Streuung der Residuen sollte über den gesamten Wertebereich konsistent sein.
- Beide Variablen sollten normalverteilt sein.
- Ihre Daten haben keine Ausreißer.
- Die Daten sollten aus einer zufälligen oder repräsentativen Stichprobe gezogen werden.
Außerdem müssen die Variablen normal verteilt und frei von Ausreißern sein, da diese die Ergebnisse verzerren können. Beide Variablen müssen kontinuierlich sein, damit die Pearson’sche Korrelation angewendet werden kann.
Der Wert des Produkt-Moment-Korrelationskoeffizienten von Pearson reicht von +1, was eine perfekte positive Korrelation anzeigt. -1 bedeutet eine perfekte negative Korrelation und 0 steht für keine Korrelation. Diese Beziehung ist symmetrisch, so dass die Reihenfolge der Variablen keine Rolle spielt.
Außerdem ist der Koeffizient einheitenfrei, so dass Sie zwischen verschiedenen Skalen vergleichen können. Pearson’s 𝑟 ist also ein gutes statistisches Maß für eine lineare Beziehung zwischen zwei kontinuierlichen Variablen.
Berechnen des Pearsonschen Korrelationskoeffizienten
Die Berechnung des Pearsonschen Korrelationskoeffizienten ist ein einfacher, aber präziser Prozess. Die Formel für den Korrelationskoeffizienten ermittelt die Beziehung zwischen den Variablen. Sie liefert Werte zwischen -1 und 1. Verwenden Sie den nachstehenden Pearson-Korrelationskoeffizienten-Rechner, um festzustellen, wie stark die beiden Variablen miteinander verbunden sind.
Die Formel für den Pearsonschen Korrelationskoeffizienten 𝑟 lautet:
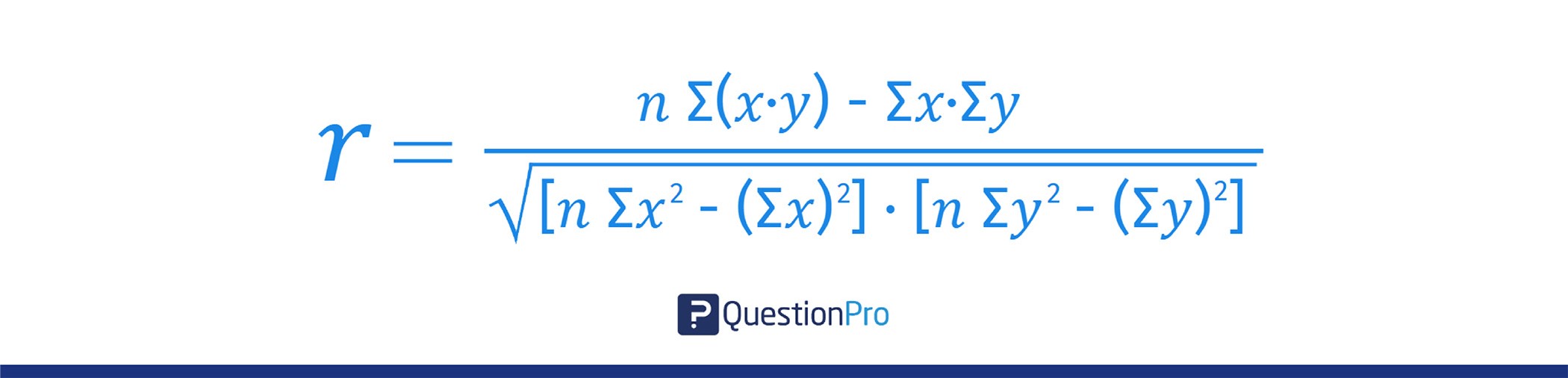
Wo:
- 𝑛: Anzahl der Datenpaare.
- ∑𝑥: Summe der 𝑥-Werte.
- ∑𝑦: Summe der 𝑦-Werte.
- ∑(𝑥⋅𝑦): Summe des Produkts der gepaarten 𝑥- und 𝑦-Werte.
- ∑𝑥2: Summe der quadrierten 𝑥-Werte.
- ∑𝑦2: Summe der quadrierten 𝑦-Werte.
Lassen Sie uns anhand eines Beispiels die Korrelation zwischen Alter und Einkommen berechnen. Organisieren Sie Ihre Daten in einer Tabelle mit beiden Variablen.
| Person | Alter (𝑥) | Einkommen (𝑦) |
| 1 | 20 | 1500 |
| 2 | 25 | 2500 |
| 3 | 30 | 3000 |
| 4 | 40 | 5000 |
| 5 | 50 | 7500 |
Fügen Sie drei zusätzliche Spalten für hinzu:
- 𝑥⋅𝑦: Das Produkt der entsprechenden 𝑥 und 𝑦 Werte.
- 𝑥2: Das Quadrat eines jeden 𝑥-Wertes.
- 𝑦2: Das Quadrat eines jeden 𝑦-Wertes.
Berechnen Sie die Werte für 𝑥⋅𝑦, 𝑥2 und 𝑦2 für jede Zeile und tragen Sie sie ein. Addieren Sie dann jede Spalte, um die Summen für ∑𝑥, ∑𝑦, ∑(𝑥⋅𝑦), ∑𝑥2 und ∑𝑦2 zu erhalten.
| Person | Alter (𝑥) | Einkommen (𝑦) | 𝑥⋅𝑦 | 𝑥2 | 𝑦2 |
| 1 | 20 | 1500 | 30000 | 400 | 2250000 |
| 2 | 25 | 2500 | 625000 | 625 | 6250000 |
| 3 | 30 | 3000 | 90000 | 900 | 9000000 |
| 4 | 40 | 5000 | 200000 | 1600 | 25000000 |
| 5 | 50 | 7500 | 375000 | 2500 | 56250000 |
| Gesamt | 165 | 19500 | 757500 | 6025 | 99000000 |
Tragen Sie die Werte aus der Tabelle ein:
- 𝑛 = 5
- ∑𝑥 = 165
- ∑𝑦 = 19500
- ∑(𝑥⋅𝑦) = 757500
- ∑𝑥2 = 6025
- ∑𝑦2 = 99000000
Setzen Sie diese Werte in die Formel ein und berechnen Sie 𝑟. Wenn das Ergebnis lautet:
- Nahe bei +1: Starke positive lineare Beziehung.
- Nahe bei -1: Starke negative lineare Beziehung.
- Nahe bei 0: Schwache oder keine lineare Beziehung.
Der Pearson-Korrelationskoeffizient (𝑟) der gegebenen Daten beträgt ungefähr 0,988. Da 𝑟 sehr nahe an +1 liegt, besteht eine starke positive lineare Beziehung zwischen den beiden Variablen(Alter und Einkommen). Das bedeutet, dass mit zunehmendem Alter das Einkommen linear ansteigt.
Hier sehen wir also, wie wichtig es ist, die Daten zu verstehen und sie richtig zu berechnen. Wenn Sie diese Schritte befolgen, können Sie Erkenntnisse aus Ihren Daten gewinnen und Entscheidungen auf der Grundlage der Stärke und Richtung der linearen Beziehungen treffen.
Sie können auch Excel verwenden, um ganz einfach Korrelationskoeffizienten zu berechnen. Alles, was Sie tun müssen, ist, Ihre Daten in zwei Spalten einzugeben und eine Zelle auszuwählen, in die Sie das Ergebnis einfügen. Um den Pearson-Korrelationskoeffizienten in Excel zu erhalten, verwenden Sie die Formel =CORREL(Bereich1, Bereich2) und wählen die richtigen Datenbereiche aus.
Spearman’s Rangkorrelationskoeffizient
Die Spearman’sche Rangkorrelation ist eine nicht-parametrische Alternative zur Pearson’schen Korrelation. Sie ist nützlich, wenn Ihre Daten die Annahmen für die Pearsonsche 𝑟 nicht erfüllen. Dieser Koeffizient ordnet die Datenpunkte der einzelnen Variablen und misst die Unterschiede zwischen diesen Rängen. Er testet, wie gut zwei Variablen durch eine monotone Funktion, nicht durch eine lineare Funktion, modelliert werden können.
Um den Spearmanschen Korrelationskoeffizienten zu verstehen, müssen Sie wissen, was eine monotone Funktion ist. Eine monotone Funktion ist eine Funktion, die niemals abnimmt oder zunimmt, wenn die Variable ‚x‘ zunimmt. Eine monotone Funktion lässt sich anhand des folgenden Bildes erklären:
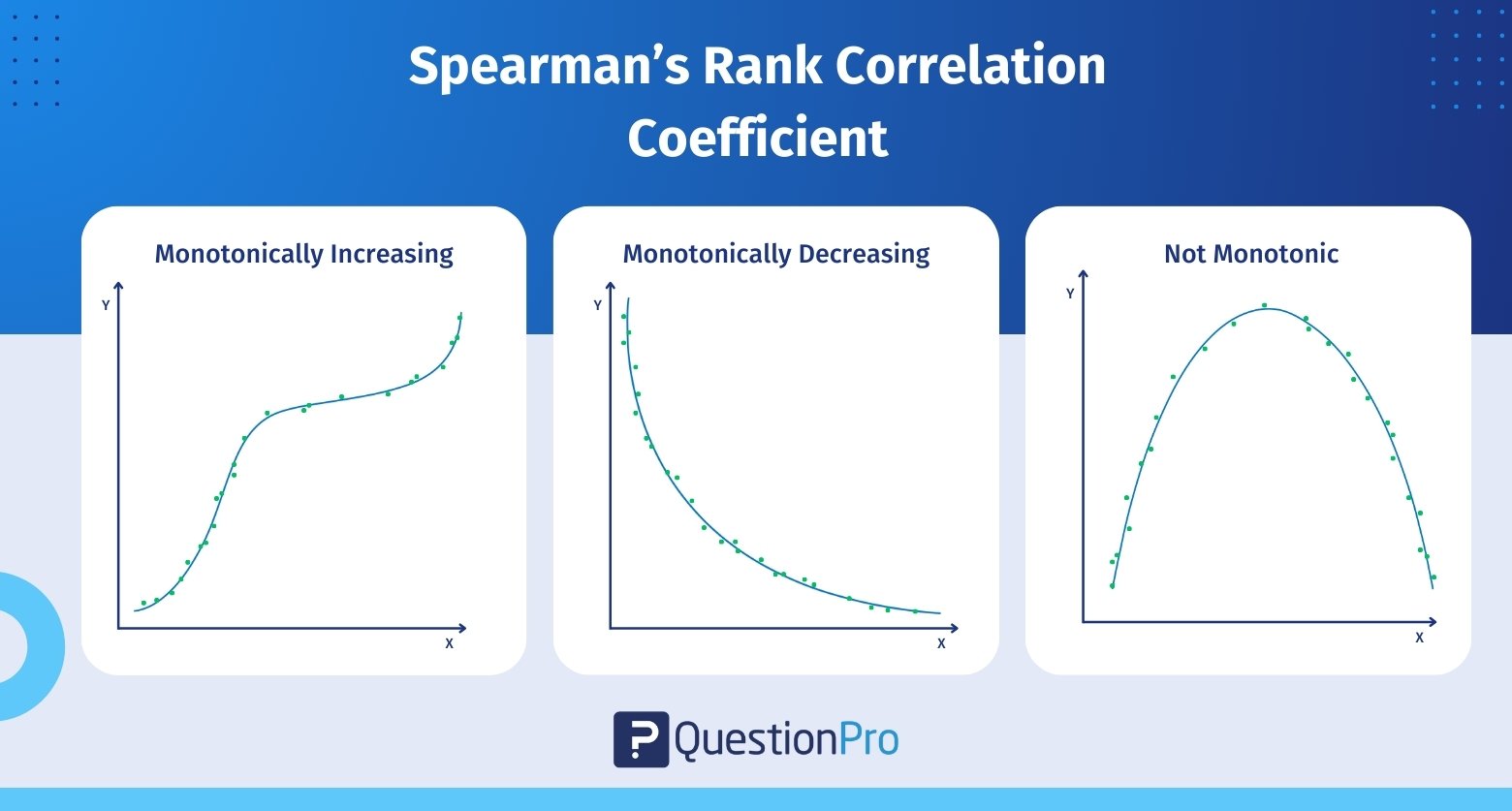
Das Bild erklärt drei Arten von monotonen Funktionen:
- Monoton steigend: Wenn ‚x‘ zunimmt und ‚y‘ niemals abnimmt.
- Monoton abnehmend: Wenn ‚x‘ zunimmt, aber ‚y‘ nie zunimmt
- Nicht monoton: Wenn ‚x‘ steigt und ‚y‘ manchmal steigt und manchmal sinkt.
Eine monotone Beziehung ist weniger restriktiv als eine lineare Beziehung, wie sie beim Pearson-Koeffizienten verwendet wird. Obwohl Monotonie keine Voraussetzung für den Spearman-Korrelationskoeffizienten ist, macht es keinen Sinn, die Spearman-Korrelation anzuwenden, wenn Sie bereits wissen, dass die Beziehung zwischen den Variablen nicht monoton ist.
Die Verwendung der Spearman’schen Rangkorrelation hilft Analysten dabei, Einblicke in die Stärke und Richtung von Beziehungen zwischen verschiedenen Datenszenarien zu gewinnen, was ihre Fähigkeit zur Interpretation der Ergebnisse verbessert.
Berechnung des Spearmanschen Rangkorrelationskoeffizienten
Die Symbole für Spearman’s rho sind ρ für den Populationskoeffizienten und 𝑟𝑠 für den Stichprobenkorrelationskoeffizienten. Die Formel für den Spearman’schen Rangkorrelationskoeffizienten lautet:
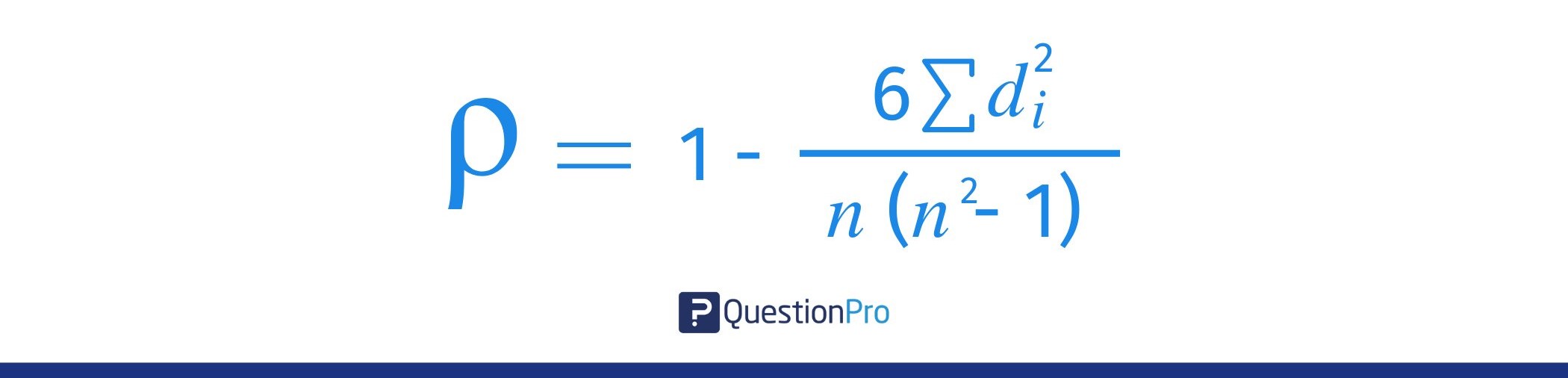
Wo:
- 𝑑𝑖: Die Differenz zwischen den Rängen der einzelnen Beobachtungspaare (𝑑𝑖=𝑅(𝑥𝑖)-𝑅(𝑦𝑖)
- 𝑛: Die Anzahl der Beobachtungen
- ∑𝑑𝑖2: Die Summe der quadrierten Unterschiede zwischen den Rängen
Um diese Formel zu verwenden, ermitteln Sie die Unterschiede (di) zwischen den Rängen Ihrer Variablen für jedes Datenpaar und verwenden diese als Haupteingabe für die Formel.
Der Spearmansche Rangkorrelationskoeffizient ρ kann einen Wert zwischen +1 und -1 annehmen, wobei:
- ρ von 1 bedeutet, dass alle Rankings für jede Variable perfekt übereinstimmen.
- ρ von -1 bedeutet, dass die Rankings in genau umgekehrter Reihenfolge sind.
- ρ von 0 bedeutet, dass keine monotone Beziehung besteht und die Variablen keine konsistente Richtung haben.
Aus diesem Grund eignet sich Spearmans rho hervorragend für ordinale Daten oder Datensätze mit Ausreißern, da es eine Nullkorrelation anzeigen kann.
Lassen Sie uns anhand eines Beispiels den Spearman’s Rank Correlation Coefficient berechnen. Wir haben die Ergebnisse von 9 Schülern in Geschichte und Geographie wie folgt:
| Geschichte | Geographie |
| 35 | 30 |
| 23 | 33 |
| 47 | 45 |
| 17 | 23 |
| 10 | 8 |
| 43 | 49 |
| 9 | 12 |
| 6 | 4 |
| 28 | 31 |
Beginnen Sie mit einer Rangfolge der Punkte für Geschichte und Geografie. Weisen Sie dem höchsten Wert den Rang „1“ zu, dem zweithöchsten den Rang „2“ und so weiter. Wenn zwei Werte gleich sind, weisen Sie ihnen den Durchschnitt der Ränge zu, die sie einnehmen würden, wenn sie unterschiedlich wären.
| Geschichte | Rang | Geographie | Rang |
| 35 | 3 | 30 | 5 |
| 23 | 5 | 33 | 3 |
| 47 | 1 | 45 | 2 |
| 17 | 6 | 23 | 6 |
| 10 | 7 | 8 | 8 |
| 43 | 2 | 49 | 1 |
| 9 | 8 | 12 | 7 |
| 6 | 9 | 4 | 9 |
| 28 | 4 | 31 | 4 |
Berechnen Sie für jedes Paar von Werten die Differenz der Ränge (𝑑) und quadrieren Sie die Differenz (𝑑2):
| Geschichte | Rang | Geographie | Rang | 𝑑 | 𝑑2 |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
Addieren Sie nun alle quadrierten Differenzen (𝑑2):
- ∑𝑑2 = 4+4+1+0+1+1+1+0+0 = 12
- Also, 𝑛 = 9
Der Spearmansche Rangkorrelationskoeffizient lautet dann:
- 𝑟𝑠 = 1 – { 6 ∑𝑑𝑖2 / 𝑛 ( 𝑛2-1 ) }
= 1 – { ( 612) / ( 9( 81-1 ) }
= 1 – {72 / 720}
= 1 – 0.1
= 0.9
Der Spearmansche Rangkorrelationskoeffizient beträgt 𝑟𝑠 = 0,9, was bedeutet, dass es eine starke positive Korrelation zwischen den Noten in Geschichte und Geografie gibt. Schüler, die in Geschichte gut abschneiden, neigen also dazu, auch in Geografie gut abzuschneiden.
Praktische Anwendungen von Korrelationskoeffizienten
Korrelationskoeffizienten werden in vielen realen Anwendungen verwendet, um Entscheidungen in verschiedenen Bereichen zu treffen. Hier sind einige von ihnen:
- Finanzen
Im Finanzwesen helfen Korrelationskoeffizienten bei der Risikobewertung und der Diversifizierung eines Portfolios, indem sie die Beziehung zwischen verschiedenen Wertpapieren analysieren. Quantitative Trader nutzen diese Koeffizienten auch, um kurzfristige Änderungen der Wertpapierkurse vorherzusagen und so ihre Handelsstrategien zu verbessern.
- Umweltforschung
Umweltstudien profitieren in hohem Maße von der Korrelationsanalyse. Zum Beispiel kann eine Korrelationskoeffizientenmatrix die signifikanten Korrelationen zwischen Spurenelementen aufzeigen. Die hohen Korrelationskoeffizienten der Spurenelemente im Gomati-Fluss weisen auf gemeinsame geogene Quellen hin, und Aluminium weist die höchste Korrelation mit Fe, Ni, Ti und Rb auf. Diese Erkenntnisse sind wichtig für das Verständnis von Umweltmustern und Quellen der Kontamination.
- Genetische Studien
Die genetische Forschung verwendet ebenfalls Korrelationskoeffizienten, um die Beziehungen innerhalb der genetischen Variationen zu analysieren. So wurden zum Beispiel bei der Untersuchung der genetischen Unterschiede in Unkrautreispopulationen Pearson-Korrelationskoeffizienten von 0,783 bis 0,895 festgestellt. Diese Analysen helfen dabei, die genetische Vielfalt und evolutionäre Trends zu verstehen.
Beschränkungen der Korrelationsanalyse
Die Korrelationsanalyse liefert zwar wertvolle Erkenntnisse, hat aber auch ihre Grenzen. Eines der wichtigsten Dinge, die Sie sich merken sollten, ist, dass Korrelation nicht gleichbedeutend mit Kausalität ist. Externe Faktoren wie Störvariablen können die Korrelation zwischen zwei Variablen falsch darstellen und zu falschen Schlussfolgerungen führen. Zum Beispiel könnte eine dritte Variable, wie heißes Wetter, die Korrelation zwischen Eiscremeverkäufen und Ertrinkungsfällen beeinflussen.
Auch der Bereich der Beobachtungen kann die Korrelationskoeffizienten beeinflussen. Eine Verengung des Datenbereichs kann den Korrelationswert verändern und manchmal die wahre Beziehung zwischen den Variablen verschleiern. Ausreißer sind ein weiteres großes Problem, da sie den Pearson-Korrelationskoeffizienten verzerren und zu falschen Interpretationen führen können. Prüfen Sie also immer die Daten und berücksichtigen Sie Ausreißer, bevor Sie Schlussfolgerungen aus der Korrelationsanalyse ziehen.
Außerdem ist die Korrelationsanalyse nur für bivariate Daten geeignet. Sie kann also keine Beziehungen bewerten, die über zwei Variablen hinausgehen. Das bedeutet, dass komplexere Beziehungen, die mehrere Variablen umfassen, andere analytische Ansätze erfordern, wie die Regressionsanalyse oder die multivariate Analyse. Außerdem können Messfehler die Zuverlässigkeit der Korrelationskoeffizienten beeinträchtigen und die beobachteten Werte aufblähen oder abschwächen.
So führen Sie einen Korrelationskoeffizienten mit QuestionPro durch
Mit dem Korrelationstool von QuestionPro können Sie die Beziehungen zwischen den Umfragevariablen leicht erkennen. Die Matrix und die Farbkodierung helfen Ihnen, positive und negative Korrelationen zu erkennen und Ihre Umfragedaten sinnvoll zu nutzen.
Um mit der Analyse von Korrelationen in Ihren Umfragedaten zu beginnen:
- Melden Sie sich bei QuestionPro an.
- Gehen Sie vom Dashboard aus zu Meine Umfragen.
- Wählen Sie die Umfrage, die Sie analysieren möchten.
- Gehen Sie zu Analytics und klicken Sie in der Dropdown-Liste auf Korrelationsanalyse.
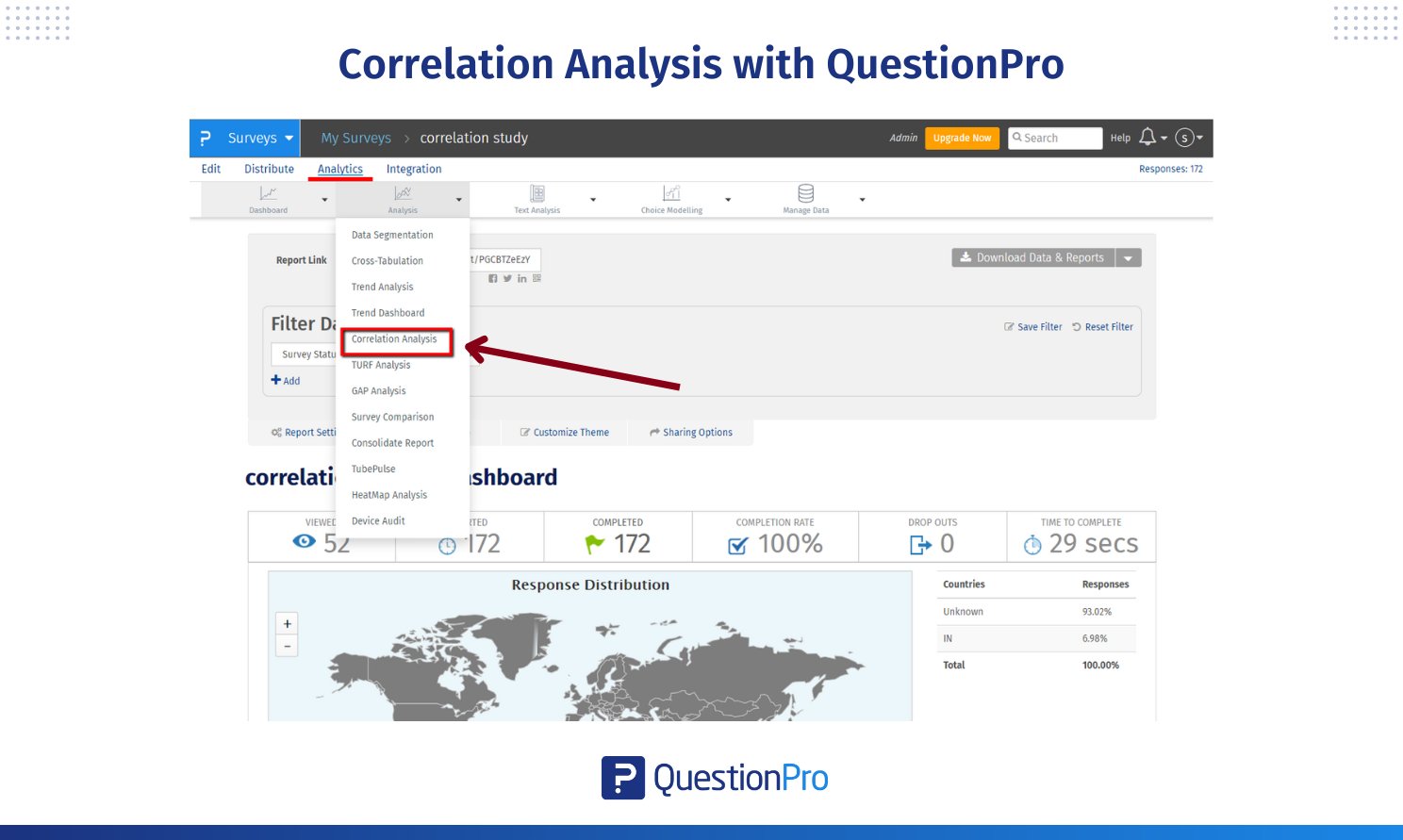
Wenn Sie das Tool zur Korrelationsanalyse öffnen, wird eine 2 × 2 Matrix angezeigt.
- Diese Matrix zeigt den Korrelationskoeffizienten für die ersten beiden Fragen in Ihrer Umfrage.
- Die Matrix hilft Ihnen, die Beziehung zwischen diesen Variablen zu erkennen.
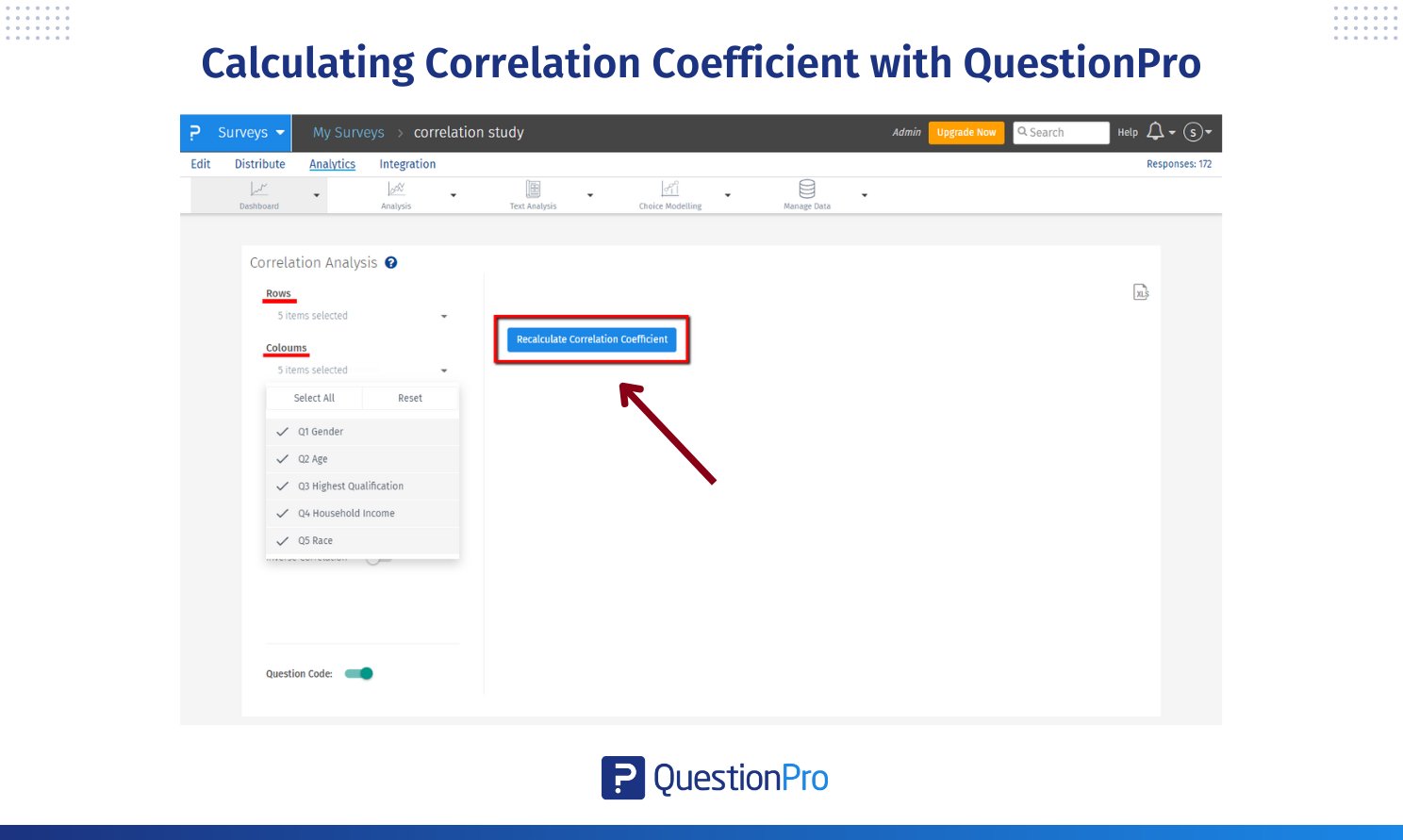
Wenn Sie andere Fragen oder die gesamte Umfrage miteinander in Beziehung setzen möchten:
- Wählen Sie in den Abschnitten Zeilen und Spalten die Fragen aus, die Sie miteinander in Beziehung setzen möchten.
- Um alle Fragen zu sehen, wählen Sie alle in den Zeilen und Spalten.
- Klicken Sie auf Korrelationskoeffizient neu berechnen, um einen neuen Korrelationsbericht zu erhalten.
Die Korrelationsmatrix verwendet eine auf Schwellenwerten basierende Farbkodierung, um die Stärke der Beziehungen leichter interpretieren zu können.
Direkte Korrelation (positiv):
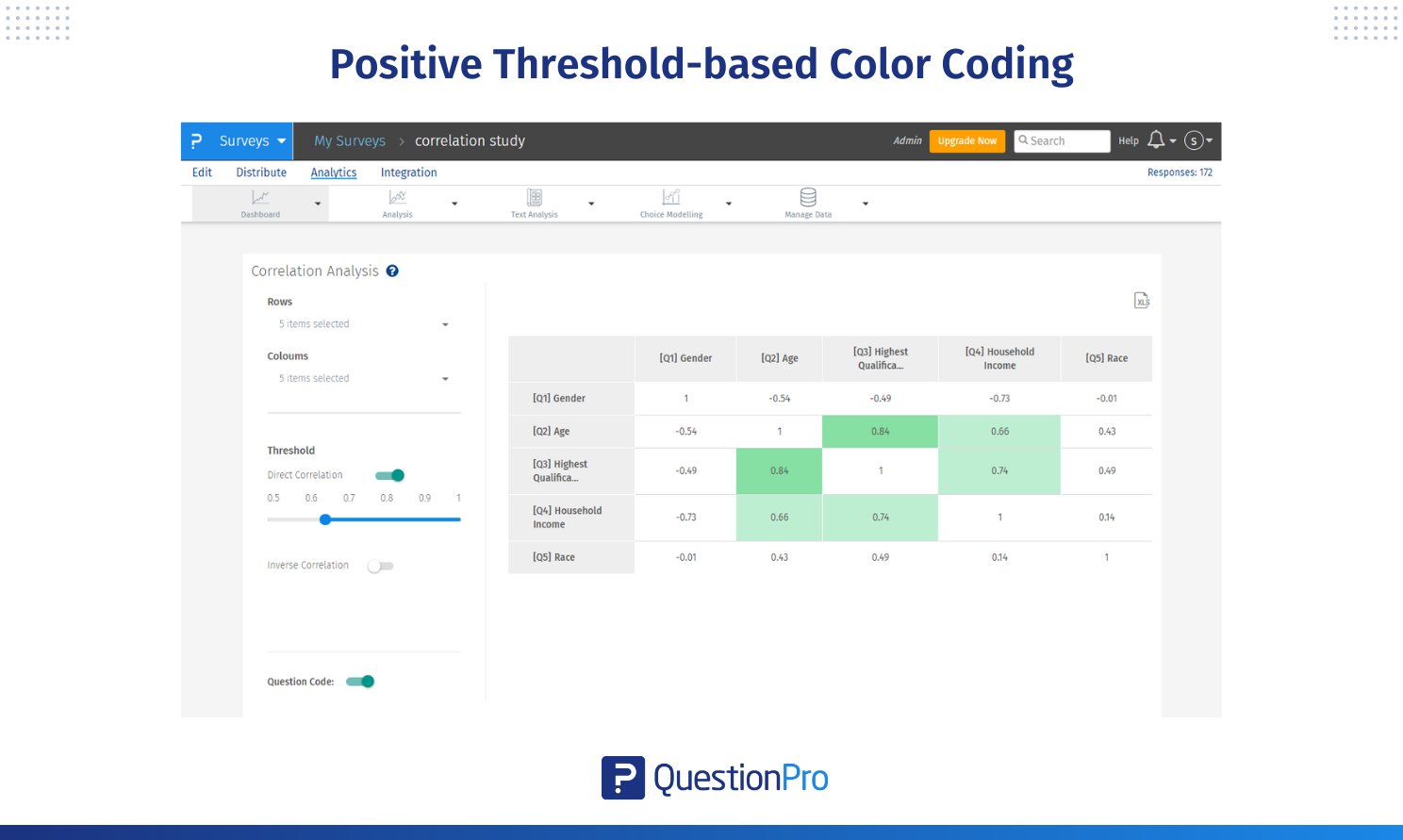
- Hellgrün: Korrelationskoeffizienten zwischen 0,65 und 0,80, was auf eine wenig starke positive Beziehung hinweist.
- Mittelgrün: Koeffizienten zwischen 0,80 und 0,90, was auf eine mittelstarke positive Beziehung hinweist.
- Dunkelgrün: Koeffizienten über 0,90, was auf eine sehr starke positive Beziehung hinweist.
Dies bedeutet, dass es einen sehr starken Zusammenhang zwischen den Variablen gibt. Jeder Anstieg einer Variable führt zu einem Anstieg einer anderen.
Wenn der Benutzer die inverse Korrelation aktiviert, werden Zellen mit inverser Beziehung hervorgehoben. Bei der inversen Korrelation haben wir ähnliche Bereiche.
Umgekehrte Korrelation (Negativ):
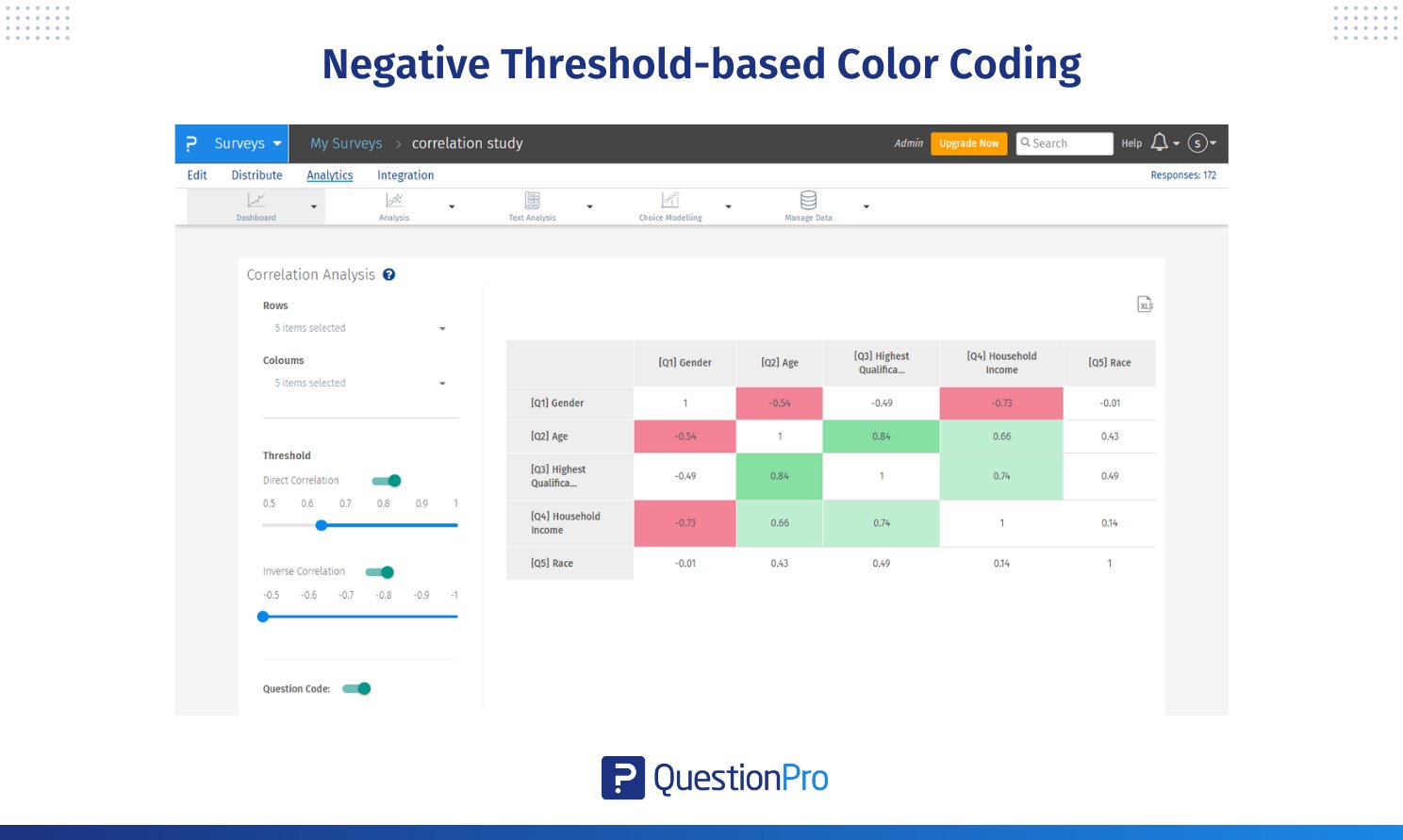
- Hellrot: Korrelationskoeffizienten zwischen -0,65 und -0,80, was auf eine wenig starke negative Beziehung hinweist.
- Mittelrot: Koeffizienten zwischen -0,80 und -0,90, was auf eine mittelstarke negative Beziehung hinweist.
- Dunkelrot: Koeffizienten unter -0,90, was auf eine sehr starke negative Beziehung hinweist.
Fazit
Korrelationskoeffizienten sind der Schlüssel zum Verständnis der Beziehungen zwischen Variablen. Wir haben die Grundlagen der Korrelationsanalyse behandelt – von der Definition des Korrelationskoeffizienten über die Interpretation der Werte bis hin zu den verschiedenen Typen wie dem Pearson-Koeffizienten und dem Spearman-Koeffizienten. Die manuelle Berechnung dieser Koeffizienten oder die Verwendung von Tools wie Excel ist eine praktische Anwendung in verschiedenen Arten von Forschung.
Die Korrelationsanalyse ist zwar wertvoll, aber sie hat ihre Grenzen. Wenn Sie diese Konzepte verstehen, können Sie Ihre Daten entschlüsseln, fundierte Entscheidungen treffen und sinnvolle Muster finden. Korrelationskoeffizienten sind mächtig, und Sie können sie nutzen, um Ihre Datenanalysefähigkeiten zu verbessern.
QuestionPro macht die Korrelationsanalyse von Umfragedaten zu einem Kinderspiel. Die Benutzeroberfläche verfügt über eine Korrelationsmatrix mit integrierter schwellenwertbasierter Farbkodierung, so dass Sie die Stärke und Richtung der Beziehungen zwischen den Variablen erkennen können. Sie können bestimmte Fragen oder alle Fragen auswählen. Die Plattform unterstützt auch umgekehrte Korrelationen, so dass Sie sowohl positive als auch negative Beziehungen sehen können.
Ganz gleich, ob Sie Kundenfeedback oder akademische Forschungsdaten analysieren, das Korrelationsanalyse-Tool von QuestionPro ist eine leistungsstarke Methode, um Muster und Beziehungen zu finden und datengestützte Entscheidungen zu treffen.
Häufig gestellte Fragen (FAQs)
Antwort: 𝑟 ist der Korrelationskoeffizient, der die Stärke und Richtung der Beziehung zwischen den Variablen anzeigt, während 𝑟², das Bestimmtheitsmaß, angibt, wie gut das Modell die Varianz in den Daten erklärt.
Antwort: 0,8 bedeutet eine ziemlich starke positive Beziehung zwischen zwei Variablen, d.h. wenn eine Variable steigt, steigt auch die andere stark an. Dies wird als eine signifikante Beziehung in den Daten betrachtet.
Antwort: Der Hauptunterschied zwischen der Pearson-Korrelation und der Spearman-Korrelation besteht darin, dass die Pearson-Korrelation lineare Beziehungen in quantitativen Daten misst, während die Spearman-Korrelation monotone Beziehungen in geordneten Daten misst und auf ordinale oder nicht-normale Daten anwendbar ist.
Antwort: Ausreißer können Korrelationskoeffizienten wie den Pearson-Koeffizienten stark verzerren und zu irreführenden Ergebnissen für die Beziehung zwischen Variablen führen. Sie müssen Ausreißer während der Korrelationsanalyse identifizieren und behandeln.
Antwort: Die Korrelation kann die Beziehung aufzeigen, aber ohne signifikante Werte und eine klare Linie in den Daten kann sie nicht zur Vorhersage verwendet werden. Seien Sie also vorsichtig, wenn Sie die Korrelation für Vorhersagen verwenden.