
Spearman correlation coefficient: Definition
The Spearman’s rank coefficient of correlation or Spearman correlation coefficient is a nonparametric measure of rank correlation (statistical dependence of ranking between two variables).
Named after Charles Spearman, it is often denoted by the Greek letter ‘ρ’ (rho) and is primarily used for data analysis.
It measures the strength and direction of the association between two ranked variables. But before we talk about the Spearman correlation coefficient, it is important to understand Pearson’s correlation first. A Pearson correlation is a statistical measure of the strength of a linear relationship between paired data.
For the calculation and significance testing of the ranking variable, it requires the following data assumption to hold true:
If your data doesn’t meet the above assumptions, then you would need Spearman’s Coefficient. It is necessary to know what monotonic function is to understand Spearman correlation coefficient. A monotonic function is one that either never decreases or never increases as it is an independent variable increase. A monotonic function can be explained using the image below:
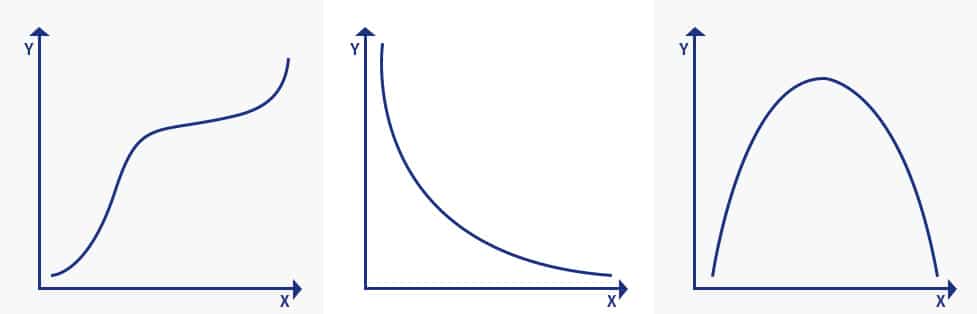
The image explains three concepts in monotonic function:
- Monotonically increasing: When the ‘x’ variable increases and the ‘y’ variable never decreases.
- Monotonically decreasing: When the ‘x’ variable increases but the ‘y’ variable never increases
- Not monotonic: When the ‘x’ variable increases and the ‘y’ variable sometimes increases and sometimes decreases.
Monotonic relation is less restrictive when compared to a linear relationship that is used in Pearson’s coefficient. Although monotonicity is not the ultimate requirement for Spearman correlation coefficient, it will not be meaningful to pursue Spearman’s correlation without actually determining the strength and direction of a monotonic relationship if it was already known that the relationship between the variable is non-monotonic.
Learn more: Correlational Research
Spearman correlation coefficient: Formula and Calculation with Example
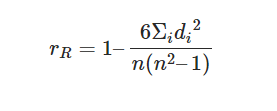
Here,
n= number of data points of the two variables
di= difference in ranks of the “ith” element
The Spearman Coefficient,⍴, can take a value between +1 to -1 where,
- A ⍴ value of +1 means a perfect association of rank
- A ⍴ value of 0 means no association of ranks
- A ⍴ value of -1 means a perfect negative association between ranks.
Closer the ⍴ value to 0, weaker is the association between the two ranks.
We must be able to rank the data before proceeding with the Spearman’s Rank Coefficient of Correlation. It is important to observe if increasing one variable, the other variable follows a monotonic relation.
At every level, you will need to compare the values of the two variables. Here is how the calculations work:
The scores of 9 students in History and Geography are mentioned in the table below.
Step 1- Create a table of the data obtained.
Step 2- Start by ranking the two data sets. Data ranking can be achieved by assigning the ranking “1” to the biggest number in the column, “2” to the second biggest number and so forth. The smallest value will usually get the lowest ranking. This should be done for both sets of measurements.
Step 3- Add a third column d to your data set, d here denotes the difference between ranks. For example, if the first student’s physics rank is 3 and the math rank is 5 then the difference in the rank is 3. In the fourth column, square your d values.
| History | Rank | Geography | Rank | d | d square |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
Step 4- Add up all your d square values, which is 12 (∑d square)
Step 5- Insert these values in the formula
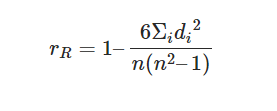
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
The Spearman’s Rank Correlation for this data is 0.9 and as mentioned above if the ⍴ value is nearing +1 then they have a perfect association of rank.
How to Conduct a correlation coefficient with QuestionPro
In this section, you will learn how you can run Spearman’s Rank Coefficient of Correlation for your survey.
Step 1: Go to My Surveys →Select Survey→Analytics
Step 2: Click on Correlational Analysis under Analysis
Step 3: Click on Generate Spearman Coefficient button to get a detailed report
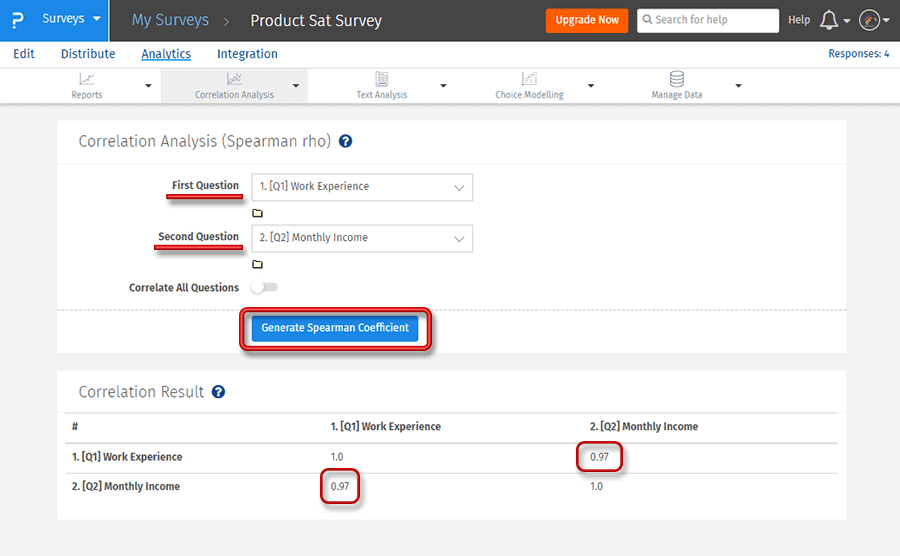
In the above example, the Spearman coefficient of correlation is used to find out the relationship between the two variables, Work experience and Monthly income. A general notion is monthly income should increase with work experience, which means there should be a positive association between the two variables which is proved by the rs value which is 0.97
Learn more: GAP Analysis- Definition, Method and Template with Example







