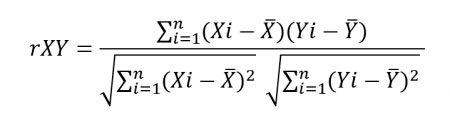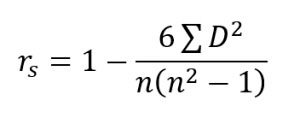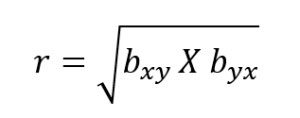El análisis de correlación es un enfoque estadístico que se utiliza para determinar la relación entre las variables cuantitativas o categóricas.
Cuando quieres determinar la correlación a través del análisis de datos, hay dos tipos de información con la que debes trabajar:
- Datos univariados: Cuando quieres trabajar con una sola variable, es necesario medir la tendencia central a preguntar por los datos representativos y conocer su desviación a través de la dispersión, medir la forma y el tamaño de la distribución a través de la asimetría y medir la concentración de datos en la posición central a través de la curtosis. Por lo tanto, los datos relativos a una sola variable se denominan datos univariados.
- Datos bivariados: El análisis de correlación se trata más bien de estudiar la relación entre dos variables al mismo tiempo.Por ejemplo, el precio de un producto y sus ventas medias, o la edad y la presión arterial de una persona. Así, dos caracteres de la misma entidad cuando se miden simultáneamente con la ayuda de un análisis estadístico, los denominamos datos bivariados.
Descubre qué es la investigación correlacional con este artículo que tenemos para ti.
Tipos de análisis de correlación
Si hay algún tipo de correlación entre dos variables, ambas se alteran juntas durante un período de tiempo. La correlación encontrada puede ser positiva o negativa, dependiendo de los valores numéricos medidos.
Análisis de correlación positiva: Cuando debido a un aumento en cualquiera de las variables, la otra variable también comienza a aumentar asegurando una correlación positiva entre ellas.
Análisis de correlación negativa: Cuando debido al aumento en cualquiera de las variables, la otra variable comienza a disminuir asegurando una correlación negativa entre ellas.
Conoce más detalles de la correlación negativa.
Métodos para realizar un análisis de correlación
En los métodos estadísticos, el coeficiente de correlación «r» mide la fuerza, dirección y extensión de la relación entre dos variables, donde el valor de «r» siempre oscilará entre +1 y -1.
Recuerda, es inútil calcular la correlación si no hay relación entre las dos variables, ya que la correlación sólo se aplica a las relaciones lineales. Por el contrario, si existe una fuerte relación entre las dos variables, pero no es lineal, la correlación recibida puede ser engañosa.
Es aconsejable que antes de llevar a cabo una investigación de correlación utilizando cualquiera de los métodos, examines primero el diagrama de dispersión.
A continuación, se presentan algunos de los métodos de correlación de coeficientes más utilizados.
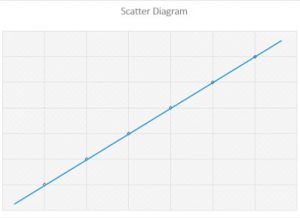
Método del diagrama de dispersión
El método del diagrama de dispersión es un enfoque utilizado para encontrar la correlación entre dos variables.
La relación entre las dos variables se presenta en forma de diagrama para comprender cuán estrechamente se relacionan entre sí.
- También, llamada gráfica de dispersión o tabla de correlación.
- El diagrama o el gráfico tiene dos variables a lo largo de sus ejes `x’ y `y’, de las cuales una es independiente y la otra es la variable dependiente.
- Es fácil predecir el comportamiento de la variable independiente dependiendo de la medida de su medida.
- Según el tipo de correlación, los diagramas de dispersión se dividen en diagramas de dispersión sin correlación, diagramas de dispersión con correlación moderada y diagramas de dispersión con una fuerte correlación.
Coeficiente de correlación de Pearson
También llamado como el “coeficiente de correlación del producto-momento”. Se define como un número entre -1 y 1 que indica el grado en que las dos variables están relacionadas linealmente.
- El método de correlación de Pearson es adecuado para variables métricas que también incluyen variables dicotómicas.
- La correlación siempre se denota como ‘»r»
- “r» es independiente de la unidad de medida.
Fórmula de correlación de Pearson
Te recomiendo leer más acerca del coeficiente de correlación de Pearson en este artículo.Coeficiente de Spearman
Es una versión no paramétrica de la correlación del coeficiente de Pearson. Este método se utiliza para medir la fuerza y dirección de la relación o asociación existente entre las dos variables.
- La letra griega “ρ” se utiliza para indicar el Coeficiente de Correlación de Spearman.
- También se indica con el símbolo rs.
- Spearman se utiliza tanto para variables ordinales como para datos continuos que han fallado en las suposiciones necesarias para llevar a cabo el coeficiente de correlación de Pearson.
Fórmula de coeficiente de Spearman
Aquí más detalles del coeficiente de correlación de Spearman.Método de los mínimos cuadrados
Es un problema matemático que se utiliza para encontrar el grado de correlación entre las dos variables utilizando la raíz cuadrada del producto de dos coeficientes de regresión, el de «x» en «y» o el de «y» en «x».
- El método del cuadrado mínimo asegura que el total del cuadrado de los errores sea lo más bajo posible.
- También se conoce como la “Línea de Mejor Ajuste”
- Se utiliza para calcular la media de los valores `x’ e `y’.
Fórmula del método de los mínimos cuadrados
Cómo utilizar el análisis de correlación en las encuestas
¿Quieres saber cómo hacer un análisis de correlación con QuestionPro? Si quieres utilizar el análisis de correlación en las encuestas que estás por aplicar, solamente debes seguir estos pasos:
- Inicia sesión en tu cuenta de QuestionPro
- Dirígete a “Encuestas”.
- Encuentra la encuesta que deseas analizar y ábrela
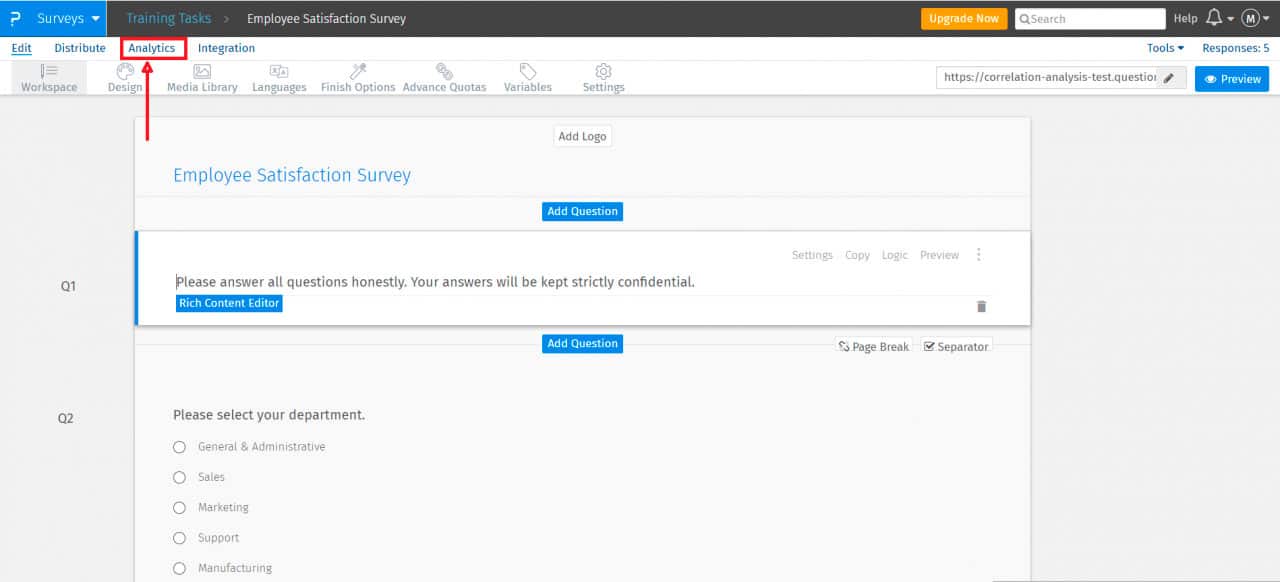
- Ve a “Análítica”.
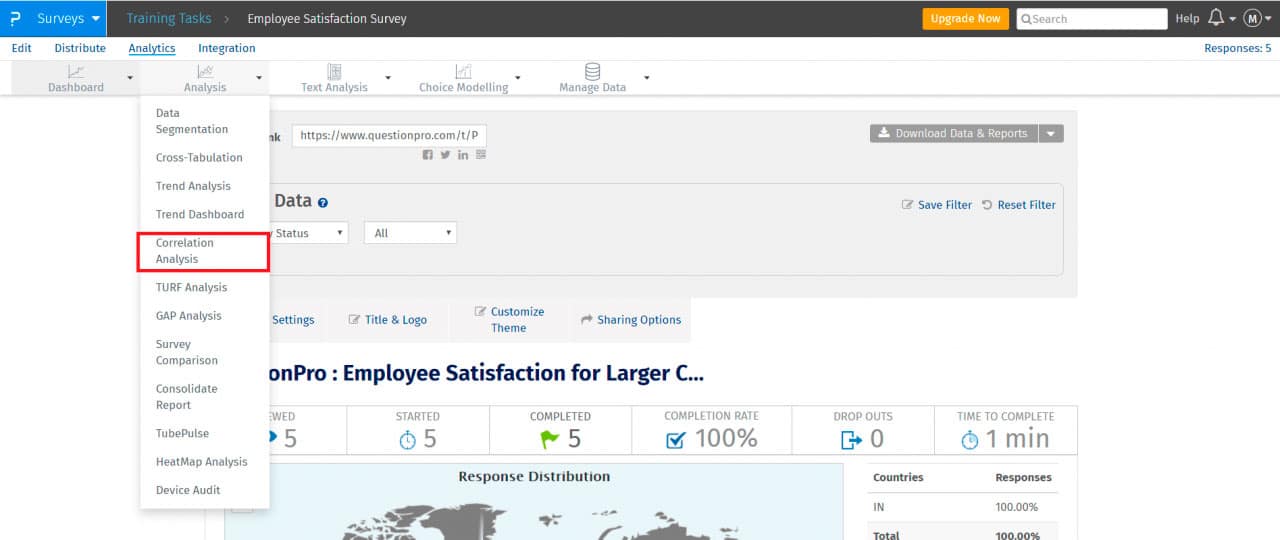
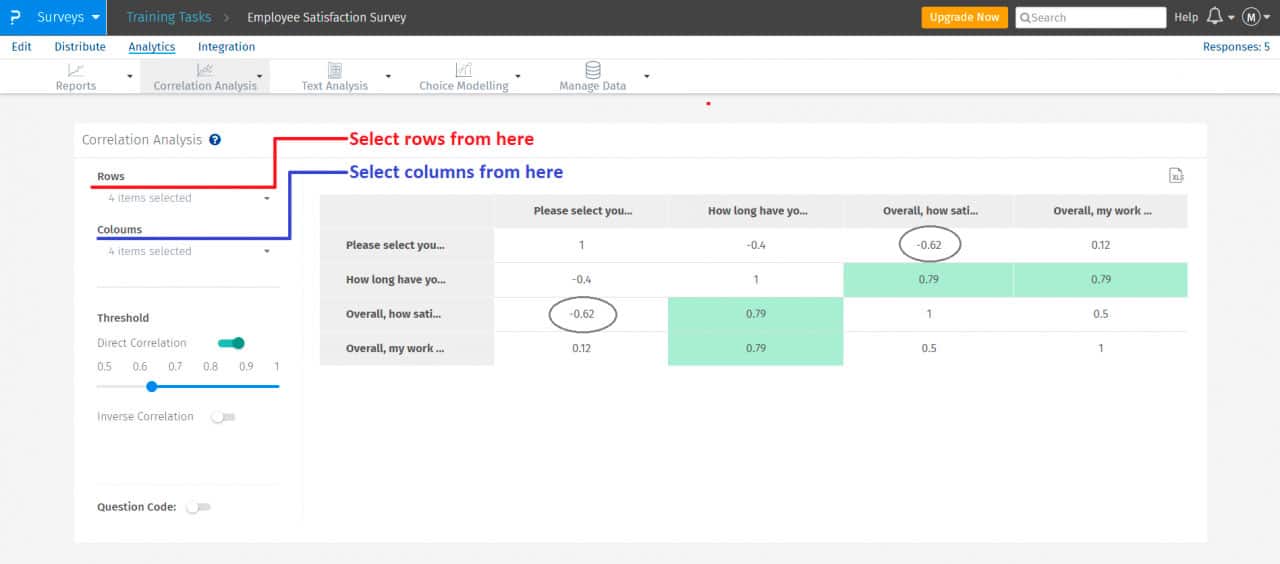
Dirígete a “Análisis de correlación”.
Si quieres conocer más sobre nuestra función de análisis de correlación en encuestas, ponte en contacto con nuestro equipo y estaremos encantados de ayudarte.