معامل ارتباط بيرسون: الصيغة وطريقة الحساب مع أمثلة عملية

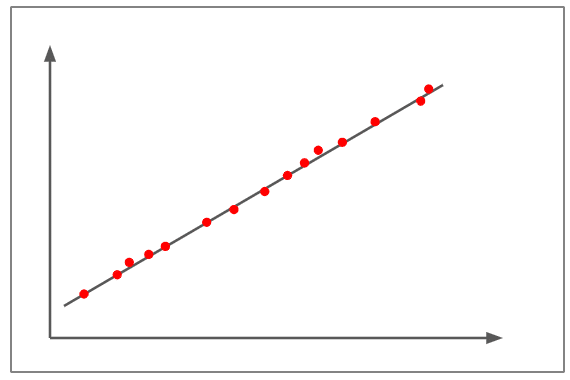
يُعد معامل ارتباط بيرسون (Pearson Correlation Coefficient) من أكثر الطرق شيوعًا في الإحصاء لقياس العلاقات الخطية بين متغيرين. حيث يساعد هذا المعامل على توضيح قوة العلاقة واتجاهها، وتكون قيمته دائمًا بين -1 و +1.

لا يقتصر استخدام معامل ارتباط بيرسون على الأبحاث الأكاديمية فقط، بل له تطبيقات عملية مهمة في مجالات مثل الاستثمار وإدارة المخاطر. على سبيل المثال، يمكن للمستثمرين الاستفادة من معامل ارتباط بيرسون عند تحليل الرسوم المبعثرة (Scatter Plots) للعوائد التاريخية بين أزواج الأصول – مثل الأسهم والسندات أو الأسهم والسلع أو السندات والعقارات – وذلك لبناء محافظ استثمارية أكثر توازنًا بين المخاطر والعوائد.

في هذا المقال، سنتعرّف على ما هو معامل ارتباط بيرسون؟، كيفية حسابه بالصيغة الرياضية، طرق تفسير نتائجه، وأهم الأمثلة العملية على استخدامه في تحليل البيانات واتخاذ القرارات المبنية على الإحصاء.

ما هو معامل ارتباط بيرسون؟

معامل ارتباط بيرسون (أو معامل بيرسون للارتباط الخطي) هو أداة إحصائية تُستخدم لقياس قوة واتجاه العلاقة بين متغيرين.

بمعنى أبسط: هو رقم يوضح تأثير تغير أحد المتغيرين على الآخر.
مثال: حتى سن معينة، يزداد طول الطفل كلما زاد عمره. (لكن طبعًا عوامل أخرى مثل الوراثة والتغذية ونمط الحياة قد تؤثر أيضًا).

يعتمد معامل بيرسون على التغاير (Covariance)، ولذلك يُعتبر من أدق الطرق لقياس العلاقة بين متغيرين.

الآن بعد أن فهمنا ماهية المعامل، لنتعرف على الحالات المناسبة لاستخدامه

إنشاء حساب مجاني

متى نستخدم معامل ارتباط بيرسون؟

يتمتع معامل ارتباط بيرسون (Pearson Correlation Coefficient) بأهمية إحصائية كبيرة، حيث يُستخدم لدراسة العلاقة بين متغيرين ومحاولة رسم خط بياني يُظهر طبيعة هذه العلاقة. ويتم قياس هذه العلاقة الخطية باستخدام آلة حاسبة معامل ارتباط بيرسون أو عبر المعادلات الإحصائية المتعارف عليها.

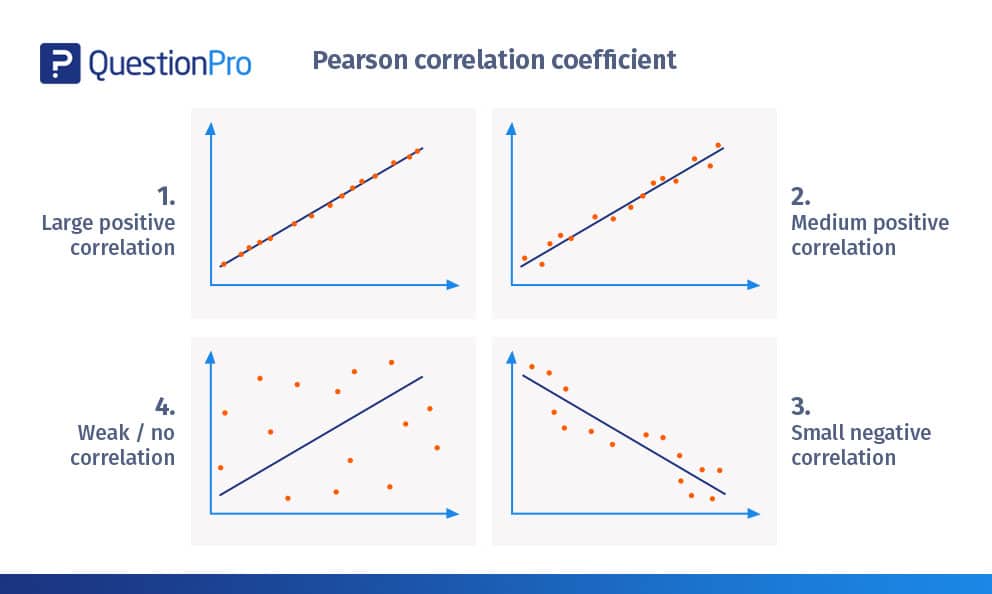
العلاقة يمكن أن تكون:

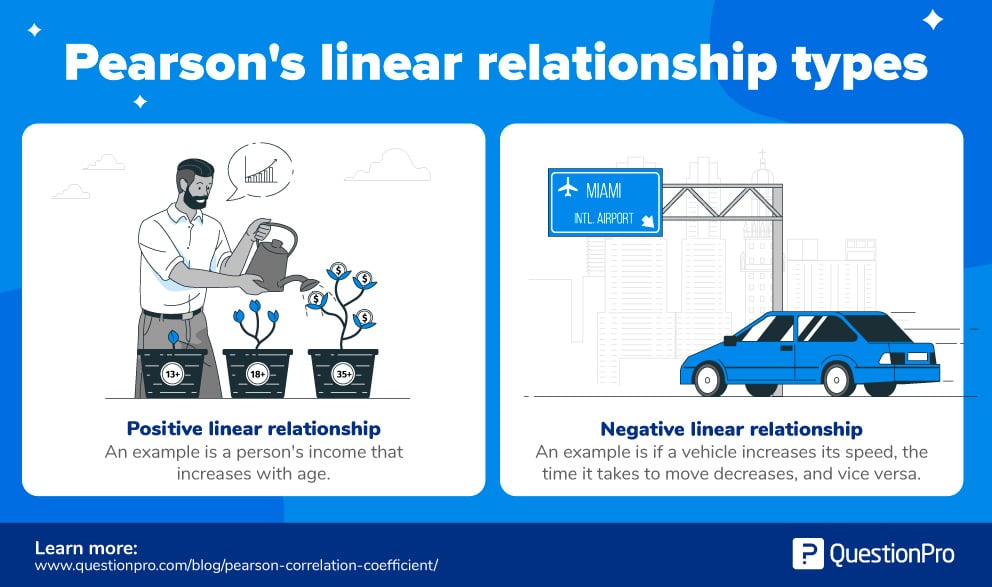
• • علاقة خطية موجبة (Positive Linear Relationship): أي أنه كلما زاد أحد المتغيرين زاد الآخر أيضًا. مثال شائع: في معظم الحالات، يزداد دخل الفرد مع التقدّم في العمر.

  • علاقة خطية سالبة (Negative Linear Relationship): أي أنه كلما زاد أحد المتغيرين قلّ الآخر. مثال: عند زيادة سرعة المركبة، يقلّ الوقت اللازم لقطع مسافة معينة، والعكس صحيح.

  من هذه الأمثلة يتضح أن معامل ارتباط بيرسون (r) يساعد على تحديد شيئين أساسيين:

  1. قوة العلاقة بين المتغيرين.

  2. اتجاه العلاقة (موجبة أم سالبة).

دعنا ننتقل إلى كيفية حسابه خطوة بخطوة.

الصيغة وطريقة الحساب

تُستخدم صيغة معامل ارتباط بيرسون (Pearson Correlation Coefficient Formula) لمعرفة العلاقة بين متغيرين، حيث تُظهر قوة واتجاه هذه العلاقة بقيمة تتراوح دائمًا بين -1 و +1. كلما اقتربت القيمة من +1 دلّ ذلك على وجود علاقة طردية قوية، وكلما اقتربت من -1 دلّ ذلك على علاقة عكسية قوية، بينما تشير القيمة القريبة من 0 إلى ضعف أو غياب العلاقة.

يمكنك استخدام حاسبة معامل ارتباط بيرسون لقياس قوة العلاقة بين متغيرين بشكل مباشر، أو الاعتماد على الصيغة الإحصائية التالية:

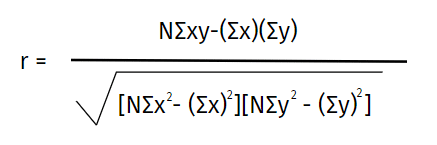
حيث:

• N = عدد أزواج القيم (Pairs of scores).

• Σxy = مجموع حاصل ضرب كل زوج من القيم (x في y).

• Σx = مجموع قيم المتغير الأول (x).

• Σy = مجموع قيم المتغير الثاني (y).

• Σx² = مجموع مربعات قيم المتغير الأول (x²).

• Σy² = مجموع مربعات قيم المتغير الثاني (y²).

هذه المكونات معًا تُمكّنك من حساب معامل ارتباط بيرسون بدقة، ومن ثم تفسير قوة واتجاه العلاقة بين المتغيرين.

حساب العلاقة بين المتغيرين — خطوة بخطوة

لفهم النتائج بشكل أفضل، يمكننا اتباع هذه الخطوات العملية لحساب المعامل.

إليك دليل خطوة بخطوة:

الخطوة الأولى: إنشاء جدول معامل الارتباط.
أنشئ جدول بيانات يتضمن كلا المتغيرين، وضع لهما تسميات x و y. أضف ثلاثة أعمدة إضافية: (xy) و (x²) و (y²). يمكنك الرجوع إلى هذا الجدول البسيط كمثال.

• الخطوة الثانية: استخدم عمليات الضرب الأساسية لإكمال الجدول.

 

 

 

 

• الخطوة الثالثة: اجمع القيم في جميع الأعمدة من الأسفل إلى الأعلى.

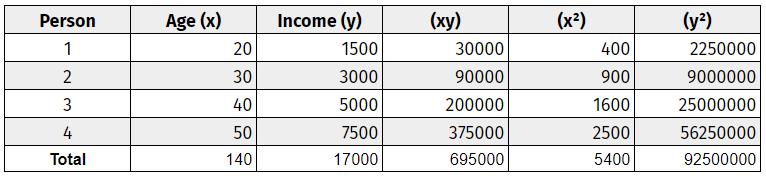
• الخطوة الرابعة: استخدم صيغة معامل الارتباط لتعويض القيم.

إذا كانت النتيجة سلبية، فهذا يعني وجود علاقة ارتباط سلبية بين المتغيرين.
أما إذا كانت النتيجة إيجابية، فهذا يشير إلى وجود علاقة ارتباط إيجابية بين المتغيرين.

كما يمكن أن توضح النتائج مدى قوة العلاقة الخطية، مثل: علاقة إيجابية قوية، علاقة سلبية قوية، علاقة إيجابية متوسطة، وهكذا.

تحديد قوة العلاقة بين المتغيرين (Pearson Correlation Coefficient)

يُستخدم معامل ارتباط بيرسون أو معامل الارتباط اللحظي للمنتج لقياس قوة العلاقة الخطية بين متغيرين.

كلما كانت العلاقة بين المتغيرين أقوى، اقتربت قيمة معامل بيرسون من +1 أو -1. الوصول إلى القيم +1 أو -1 يعني أن جميع نقاط البيانات تقع على خط مستقيم يمثل “أفضل خط ملاءمة”، أي أن التغير في أي متغير لا يضعف الارتباط مع المتغير الآخر.

أما إذا كانت النتيجة قريبة من 0، فهذا يدل على وجود تباين أكبر وضعف في العلاقة الخطية بين المتغيرين.

كيف نفسر العلاقة بين المتغيرين؟

فيما يلي بعض الإرشادات المقترحة لتفسير معامل ارتباط بيرسون: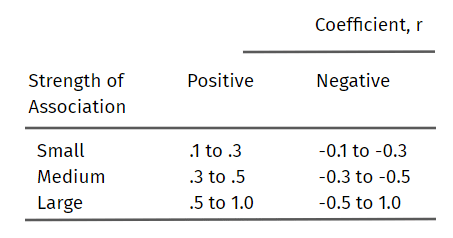

ملاحظات 

• يجب الانتباه إلى أن قوة الارتباط بين المتغيرات تعتمد على ما يتم قياسه بالإضافة إلى حجم العينة المستخدمة.

• على الرسم البياني يمكن ملاحظة العلاقة بين المتغيرين وتكوين افتراضات حتى قبل حسابها.

• إذا كانت المخططات المبعثرة (Scatterplots) قريبة من الخط، فهذا يشير إلى علاقة قوية بين المتغيرات.

• كلما اقتربت النقاط من الخط، زادت قوة العلاقة، وكلما ابتعدت عنه، أصبحت العلاقة أضعف.

• أما إذا كان الخط قريبًا من أن يكون موازيًا لمحور x وكانت النقاط مبعثرة عشوائيًا، فيمكن القول إن الارتباط بين المتغيرين شبه منعدم.

ماذا يعني مصطلحا “القوة” و”الاتجاه”؟

مصطلح “القوة” و “الاتجاه” لهما دلالة إحصائية. فيما يلي شرح مباشر لكلمتين:

• ما المقصود بالقوة (Strength)؟
  القوة تشير إلى مدى ثبات العلاقة بين متغيرين. أي: إلى أي درجة يمكن أن يتغير متغير معين بشكل متناسب مع التغير في المتغير الآخر. كلما اقتربت القيمة من +1 أو -1 دلّ ذلك على علاقة قوية، بينما تشير القيم القريبة من 0 إلى علاقة ضعيفة أو شبه منعدمة.

• ما المقصود بالاتجاه (Direction)؟
  الاتجاه يوضح ما إذا كانت العلاقة بين المتغيرين موجبة أم سالبة:

  • إذا كان الخط صاعدًا، فهذا يعني أن العلاقة موجبة: زيادة أحد المتغيرين تؤدي إلى زيادة الآخر.

  • إذا كان الخط هابطًا، فهذا يعني أن العلاقة سالبة: زيادة أحد المتغيرين تؤدي إلى انخفاض الآخر.

أمثلة على معامل ارتباط بيرسون

ما هي أمثلة معامل ارتباط بيرسون؟
لنلقِ نظرة على بعض الأمثلة المرئية التي تساعد على تفسير جدول معامل الارتباط:

• ارتباط إيجابي قوي:

• 
  

مثال على ارتباط إيجابي قوي

• يوضح الشكل أعلاه وجود ارتباط يقارب +1.

• تظهر المخططات المبعثرة وكأنها مرسومة تقريبًا على خط مستقيم.

• الميل موجب، أي أن زيادة أحد المتغيرين تؤدي إلى زيادة المتغير الآخر، وهو ما يمثل علاقة خطية موجبة.

• هذا يعني أن التغير في متغير معين يتناسب طرديًا مع التغير في المتغير الآخر.

• مثال عملي: مع نمو الأطفال، تزداد مقاسات ملابسهم وأحذيتهم.

• ارتباط إيجابي متوسط:
  

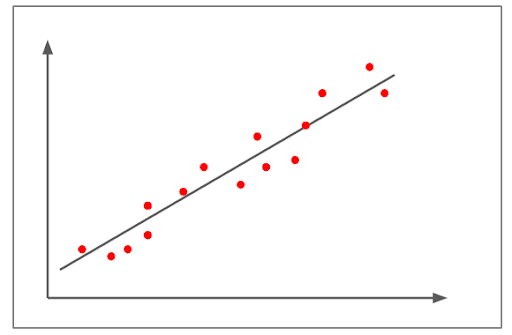
مثال على ارتباط إيجابي متوسط

• يوضح الشكل أعلاه وجود ارتباط إيجابي.

• قيمة معامل الارتباط أعلى من +0.8 ولكنها أقل من +1.

• يُظهر النمط خطًا صاعدًا قويًا نسبيًا، مما يدل على علاقة خطية متينة بين المتغيرين.

• مثال عملي: مع زيادة عدد السيارات، يزداد الطلب على الوقود.

• ارتباط سلبي ضعيف
  

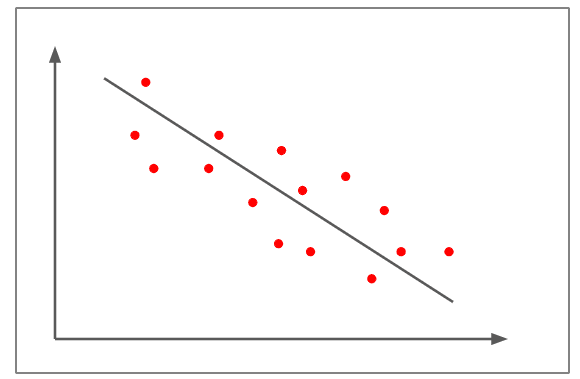
• في الشكل أعلاه، النقاط المبعثرة ليست قريبة من الخط المستقيم مثل الأمثلة السابقة.

• يوضح الشكل ارتباط خطي سلبي يقارب -0.5.

• يعني أن التغير في أحد المتغيرات عكسي مع التغير في المتغير الآخر (الميل سالب).

• مثال تطبيقي: كلما أكل الشخص أكثر → قلّ شعوره بالجوع.

• ضعف / عدم وجود ارتباط
  

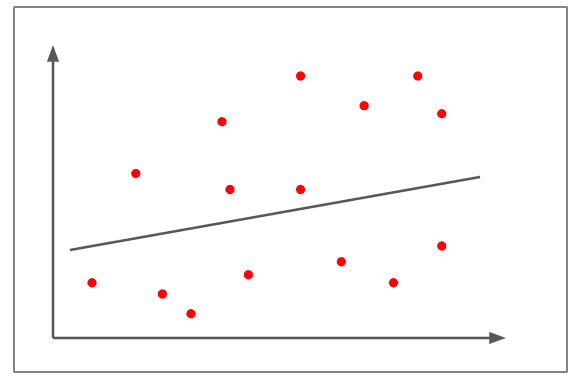
في الشكل أعلاه:

• النقاط المبعثرة بعيدة جدًا عن الخط المستقيم.

• من الصعب عمليًا رسم خط واضح يمر بينها.

• قيمة معامل الارتباط تقريبًا +0.15.

• لا يمكن الحكم ما إذا كان التغير في أحد المتغيرات يتناسب طرديًا أو عكسيًا مع التغير في المتغير الآخر.

• مثال على ارتباط ضعيف أو معدوم: ارتفاع أسعار الوقود يؤدي إلى انخفاض عدد الأشخاص الذين يتبنون الحيوانات الأليفة.

قبل الخاتمة، من المهم معرفة الفرق بين اختبار T والمعامل لضمان استخدام الطريقة الصحيحة.

اختبار T مقابل معامل ارتباط بيرسون: ما الفرق؟

عند تحليل البيانات، من المهم اختيار الأسلوب الإحصائي المناسب حسب الهدف من الدراسة. قد يبدو اختبار T ومعامل ارتباط بيرسون متشابهين، لكن لكل منهما وظيفة مختلفة:

• اختبار T (T-test): يُستخدم لمقارنة متوسط مجموعتين لمعرفة ما إذا كان بينهما فرق ذو دلالة إحصائية.

• معامل ارتباط بيرسون: يُستخدم لقياس قوة واتجاه العلاقة بين متغيرين مستمرين.

بشكل مبسط: استخدم اختبار T عند مقارنة المجموعات، بينما يُستخدم ارتباط بيرسون عند استكشاف العلاقات بين المتغيرات.

الخلاصة حول معامل ارتباط بيرسون (Pearson’s r)

معامل ارتباط بيرسون هو أداة إحصائية مهمة تساعد الباحثين والمحللين على قياس قوة واتجاه العلاقة بين متغيرين. من خلال جمع البيانات عبر الاستبيانات وتحليلها، يمكن معرفة ما إذا كان الارتباط إيجابيًا أم سلبيًا ومدى قوته.

باستخدام QuestionPro Research Suite، يمكنك جمع البيانات اللازمة لتحليل معامل الارتباط بسهولة. بعد تصدير بيانات الاستبيان من QuestionPro واستيرادها إلى جدول بيانات أو برنامج إحصائي، يمكنك إجراء تحليل الارتباط مباشرة.

يوفر لك QuestionPro أيضًا أدوات تحليل بيانات متقدمة مثل:

• الجداول التوافقية (Cross-tabulation)

• تصورات البيانات (Data Visualization)

• الاختبارات الإحصائية (Statistical Testing)

كل هذه الأدوات تساعدك على فهم العلاقات بين متغيراتك بشكل أفضل.

بهذا، تستطيع ليس فقط حساب معامل ارتباط بيرسون بدقة، بل أيضًا الحصول على رؤى أعمق تساعدك على اتخاذ قرارات مبنية على البيانات.

 هل تريد تعزيز أبحاثك وتحليلاتك الإحصائية؟
ابدأ الآن تجربة مجانية مع QuestionPro واكتشف كيف يمكن أن يساعدك في حساب معامل ارتباط بيرسون وتحليل علاقات المتغيرات بسهولة.

الأسئلة الشائعة (FAQs)