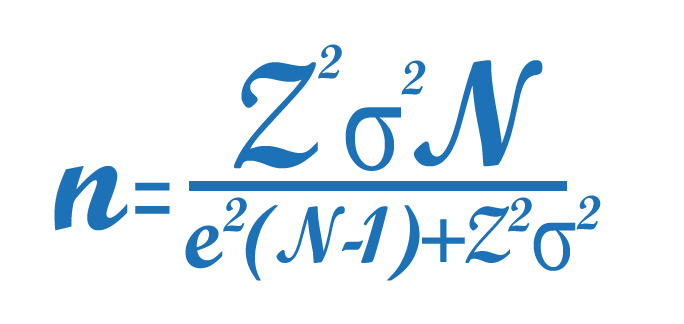Una ricerca è composta da diverse fasi che permettono di raggiungere il risultato desiderato; all’interno di questa metodologia c’è un elemento che è di vitale importanza per la ricerca stessa, ovvero determinare la dimensione di un campione di popolazione.
Che cos’è un campione di popolazione?
Un campione di popolazione è un insieme di elementi che rappresentano l’universo totale, cioè sono una frazione del numero totale di individui da valutare.
Stabilire le dimensioni del campione è un processo importante in tutte le ricerche, in quanto consente di realizzare uno studio valido e credibile, sempre vincolato agli obiettivi dello studio e alle diverse caratteristiche di ogni popolazione.
Determinare le dimensioni di un campione consente di risparmiare risorse finanziarie e umane, oltre a ridurre notevolmente il tempo necessario per svolgere la ricerca che stai conducendo, che può essere di qualsiasi tipo, come studi di opinione o ricerche di mercato.
Come determinare le dimensioni del campione della popolazione?
Esistono diversi modi per ottenere la dimensione di un campione a seconda dei dati disponibili, ad esempio, nel caso in cui si disponga del numero di persone da studiare (ad esempio, il numero di abitanti della città X), si dice che abbiamo un universo finito; in questa occasione ci occuperemo di questo tipo di universi e di come ottenere la dimensione ideale di un campione, per ottenere ciò utilizziamo la seguente formula proposta da Murray e Larry (2005):
Dove:
n = è la dimensione del campione di popolazione da ottenere.
N = è la dimensione della popolazione totale.
σ = rappresenta la deviazione standard della popolazione. Nel caso in cui non sia nota, è comune utilizzare un valore costante che è 0,5
Z = è il valore ottenuto utilizzando i livelli di confidenza. Il suo valore è una costante, di solito ci sono due valori a seconda del grado di confidenza desiderato: il 99% è il valore più alto (questo valore equivale a 2,58) e il 95% (1,96) è il valore minimo accettato per considerare la ricerca affidabile.
e = rappresenta il limite accettabile dell’errore di campionamento, generalmente compreso tra l’1% (0,01) e il 9% (0,09), con il 5% (0,5) come valore standard utilizzato nella ricerca.
Una volta stabiliti i valori appropriati, si sostituiscono i valori e si applica la formula per ottenere la dimensione del campione di popolazione corrispondente all’universo finito determinato.
Una volta eseguito il processo matematico, si otterrà il campione che, come detto all’inizio, ci aiuterà a svolgere un’indagine valida e completa.