
Il coefficiente di correlazione di Spearman è una misura non parametrica della correlazione di rango (dipendenza statistica del rango tra due variabili). Viene utilizzato principalmente per l’analisi dei dati.
Misura la forza e la direzione dell’associazione tra due variabili classificate. Ma prima di parlare della correlazione di Spearman, è importante capire la correlazione di Pearson, che è una misura statistica della forza di una relazione lineare tra dati appaiati.
Per il calcolo e il test di significatività della variabile di ranking, è necessario che siano vere le seguenti ipotesi sui dati:
- Livello o rapporto di intervallo
- Relazione lineare
- Distribuito bivariato
Se i tuoi dati non soddisfano i presupposti di cui sopra, avrai bisogno del coefficiente di correlazione di Spearman. A tal fine, è necessario sapere cos’è la funzione monotona per comprenderla.
Una funzione monotona è una funzione che non diminuisce e non aumenta mai, poiché la variabile indipendente è crescente. Può essere spiegata utilizzando l’immagine seguente:
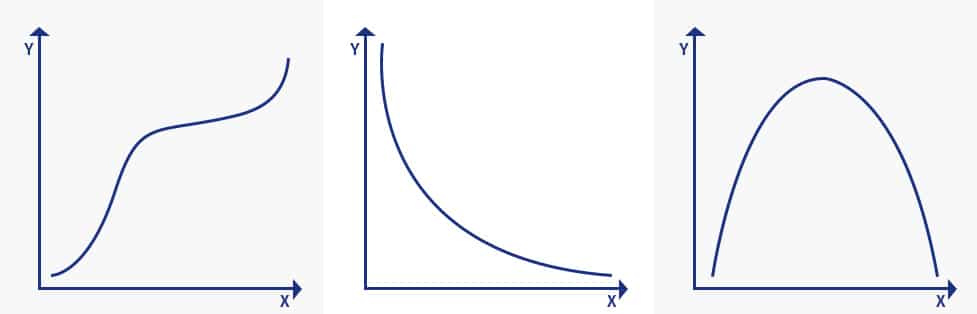
L’immagine spiega tre concetti della funzione monotona:
- Monotonicamente crescente: quando la variabile “x” aumenta e la variabile “y” non diminuisce mai.
- Monotonicamente decrescente: Quando la variabile “x” aumenta ma la variabile “y” non aumenta mai.
- Non monotono: quando la variabile “x” aumenta e la variabile “y” a volte aumenta e a volte diminuisce.
La relazione monotonica è meno restrittiva rispetto alla relazione lineare utilizzata nel coefficiente di correlazione di Pearson. Anche se la monotonicità non è un requisito fondamentale, non ha senso perseguirla senza determinare effettivamente la forza e la direzione di una relazione monotona se si sa già che la relazione tra le variabili non è monotona.
Come calcolare il coefficiente di correlazione di Spearman
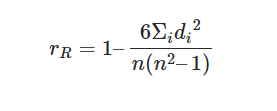
n= numero di punti dati delle due variabili
di= differenza di rango dell’elemento “n”.
Il Coefficiente di Spearman,⍴, può assumere un valore compreso tra +1 e -1 dove,
- Un valore di +1 in ⍴ significa un’associazione di rango perfetta.
- Un valore di 0 in ⍴ significa che non c “è un” associazione di gamma.
- Un valore di -1 in ⍴ indica una perfetta associazione negativa tra i ranghi.
Se il valore di ⍴ è vicino a 0, l’associazione tra i due ranghi è più debole.
Dobbiamo essere in grado di classificare i dati prima di procedere con il coefficiente di correlazione di Spearman. È importante notare che se una variabile aumenta, l’altra segue una relazione monotona.
Come si utilizza il coefficiente di correlazione di Spearman
Ad ogni livello, dovrai confrontare i valori delle due variabili. Ecco un esempio di come funzionano i calcoli:
I risultati di 9 studenti in Storia e Geografia sono riportati nella seguente tabella.
Passo 1: Crea una tabella con i dati ottenuti.
Passo 2: Inizia ordinando i due gruppi di dati. La classificazione dei dati può essere ottenuta assegnando la posizione “1” al numero più grande della colonna, “2” al secondo numero più grande e così via. Il valore più piccolo sarà generalmente quello più basso. Questa operazione deve essere eseguita per entrambe le serie di misurazioni.
Passo 3: Aggiungi una terza colonna “d” al tuo set di dati: “d” indica la differenza tra le classifiche. Ad esempio, se la classifica di fisica del primo studente è 3 e quella di matematica è 5, la differenza di classifica è 3. Nella quarta colonna, eleva al quadrato i valori “d”.
| La storia | Gamma | Georgrafia | Gamma | d | d quadrato |
|---|---|---|---|---|---|
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
Passo 4: Somma tutti i valori del quadrato “d” che è 12 (∑d al quadrato).
Passo 5: Inserisci questi valori nella formula.
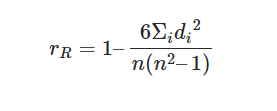
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
Il coefficiente di correlazione di Spearman per questi dati è pari a 0,9 e, come già detto, se il valore ⍴ è prossimo a +1 allora si ha un’associazione di rango perfetta.
Come eseguire il coefficiente di correlazione di Spearman con QuestionPro
In questa sezione scoprirai come eseguire il coefficiente di correlazione di Spearman nel tuo sondaggio online. sondaggio online.
Passo 1: vai a Le mie indagini → seleziona l’indagine → Analisi.
Passo 2: Clicca su Analisi di correlazione
Fase 3: Clicca sul pulsante Genera il Coefficiente di Spearman per ottenere un rapporto dettagliato.
Nell “esempio precedente, il coefficiente di correlazione di Spearman viene utilizzato per scoprire la relazione tra le due variabili, esperienza lavorativa e reddito mensile. L” idea generale è che il reddito mensile dovrebbe aumentare con l “esperienza lavorativa, il che significa che dovrebbe esserci un” associazione positiva tra le due variabili, come dimostra il valore di rs che è 0,97.
Se vuoi utilizzare questa o altre funzioni della nostra piattaforma per un progetto di ricerca, non esitare a contattare uno dei nostri esperti.



