
- Custom Variable Widget
- Priority Matrix
- Heatmap Widget
- Grid Widget
- Weighted mean widget
- Comment List widget
- Widget Filters
- Ranking List Widget
- Distribution Chart
- NPS Widget
- Trend Widget
- Word Cloud Widget
- Cross tab widget
- KPI Comparison Widget
- Bubble chart
- Custom Metric Trend Chart
- Trend Comparison Widget
CX - Correlation Analysis (Spearman rho) - FAQ?
-
In general,
- rs > 0 implies positive agreement among ranks
- rs < 0 implies negative agreement (or agreement in the reverse direction)
- rs = 0 implies no agreement
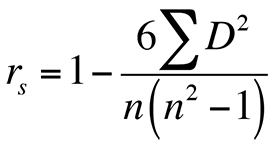
- rs = Spearman rank correlation
- D = the difference between the ranks of corresponding variables
- n = number of observations
Go to: My Surveys » Select Survey » Analytics
Click on Correlation Analysis under the Analysis drop down.-
By default, we display 2*2 matrix which shows the corelation coeffecient of first 2 questions of the survey.
To Correlate other questions:
- Select the questions in Rows and columns that you wish to correlate. You can also select all questions.
- Click on Recalculate correlation coeffecient button to generate the report.
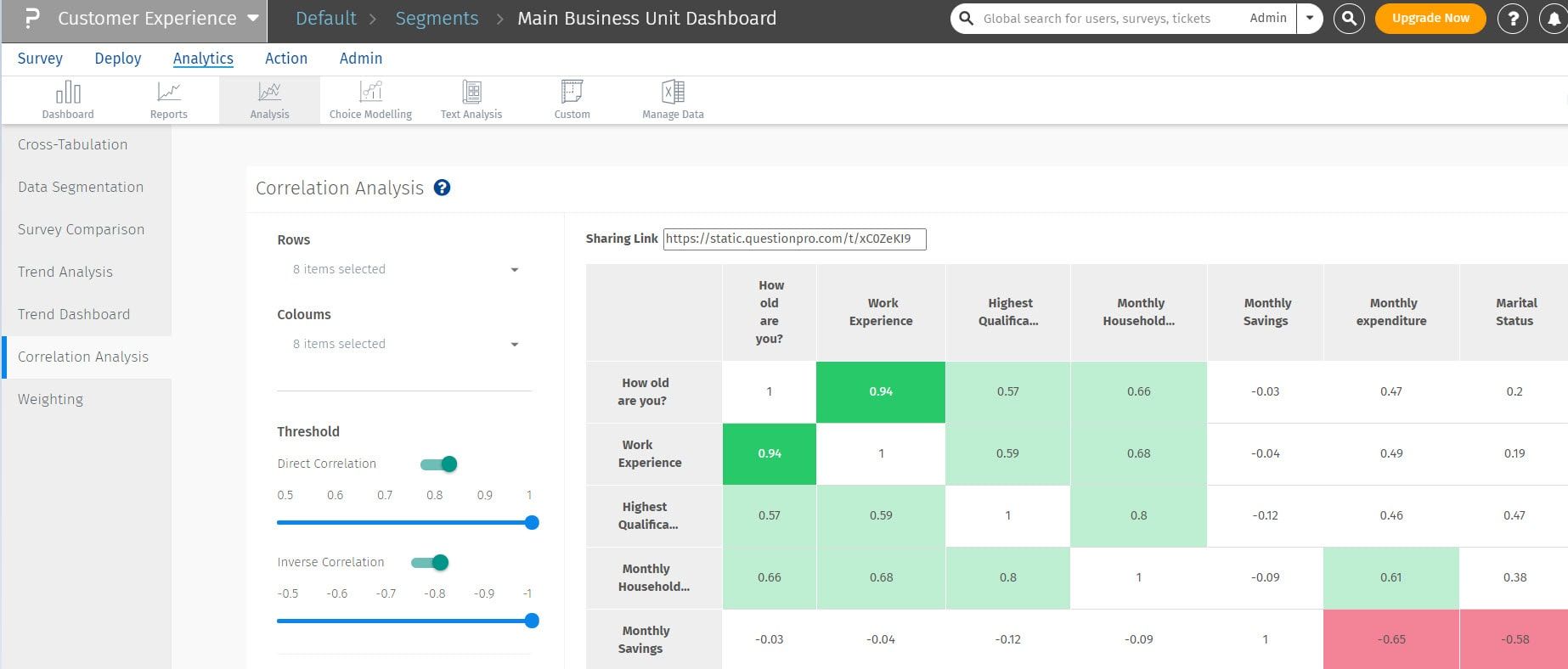
Threshold section help user with the color coding of the cells which indicates the strength of the relationship between the variables. Direct correlation will have deafult set threshold to 0.65 and has 3 colors. If correlation coeffecient value is below 0.80 to 0.65(set threshold) cell will be colored with light green indicating low strength of relationship. If the value is between 0.80 to 0.90 cell is colored with medium green and if value is above 0.90 cell is colored with dark green indicating high strength of correlation between 2 variables.
When user enables inverse correlation, Cells with inverse relation gets highlighted. We have similar buckets in inverse correlation. If correlation coeffecient value is below -0.80 to -0.65(set threshold) cell will be colored with light red indicating low strength of relationship. If the value is between -0.80 to -0.90 cell is colored with medium red and if value is above -0.90 cell is colored with dark red indicating high strength of correlation between 2 variables.
Excel download with color coding of the cells is supported for the correlation analysis.Single select and multi choice questions are supported for correlation analysis.

