Conjoint Analysis – Profiles

Profiles in a Conjoint question type are different configurations that are presented to respondents. Each profile is a combination of different levels of various attributes (For example, Brand, Cost, Features). By evaluating these profiles, respondents reveal their preferences and trade-offs, allowing researchers to estimate the relative importance of each attribute and its levels in influencing consumer choice.

With QuestionPro, you can access Profiles in a Conjoint question type as shown below: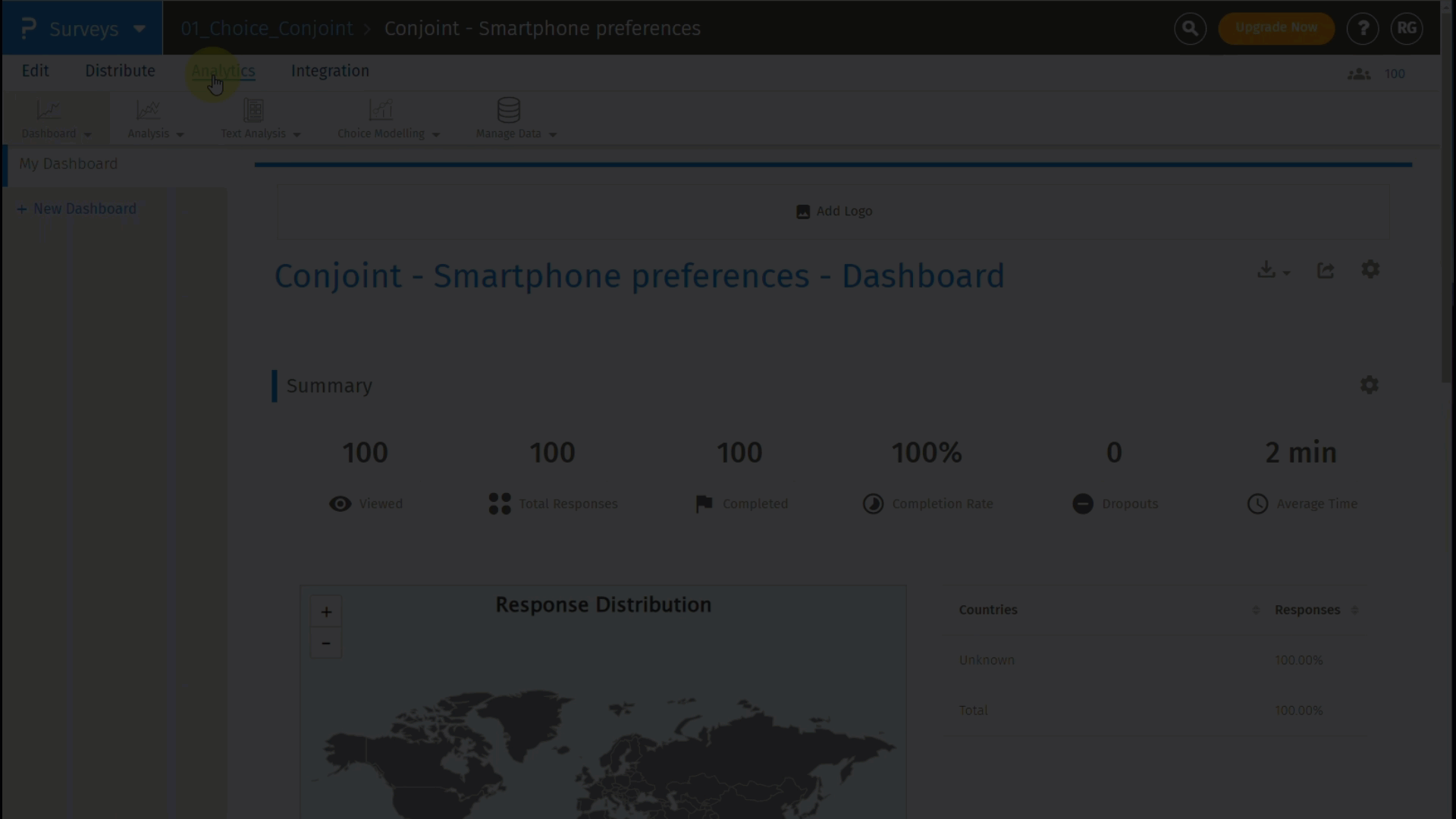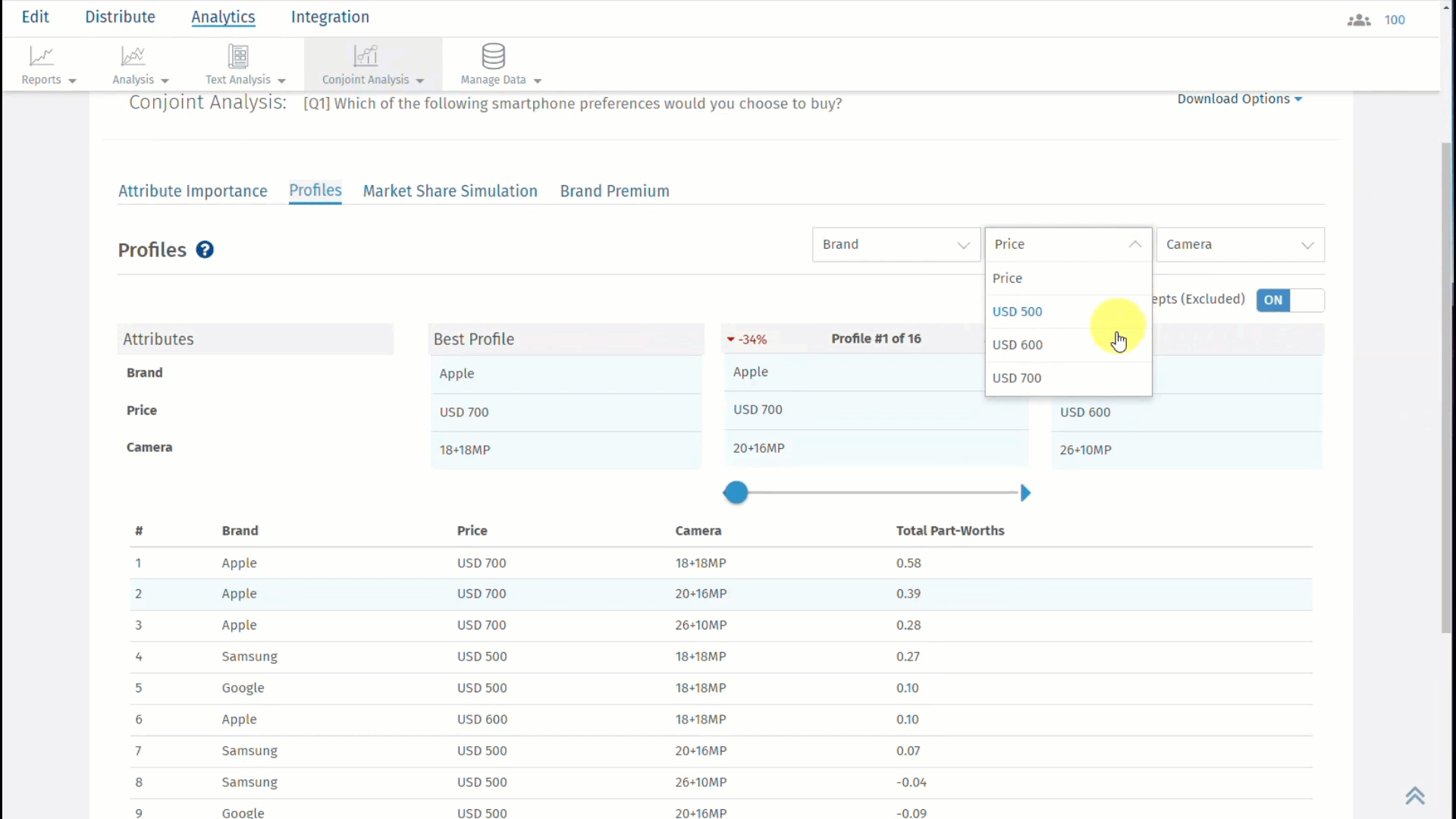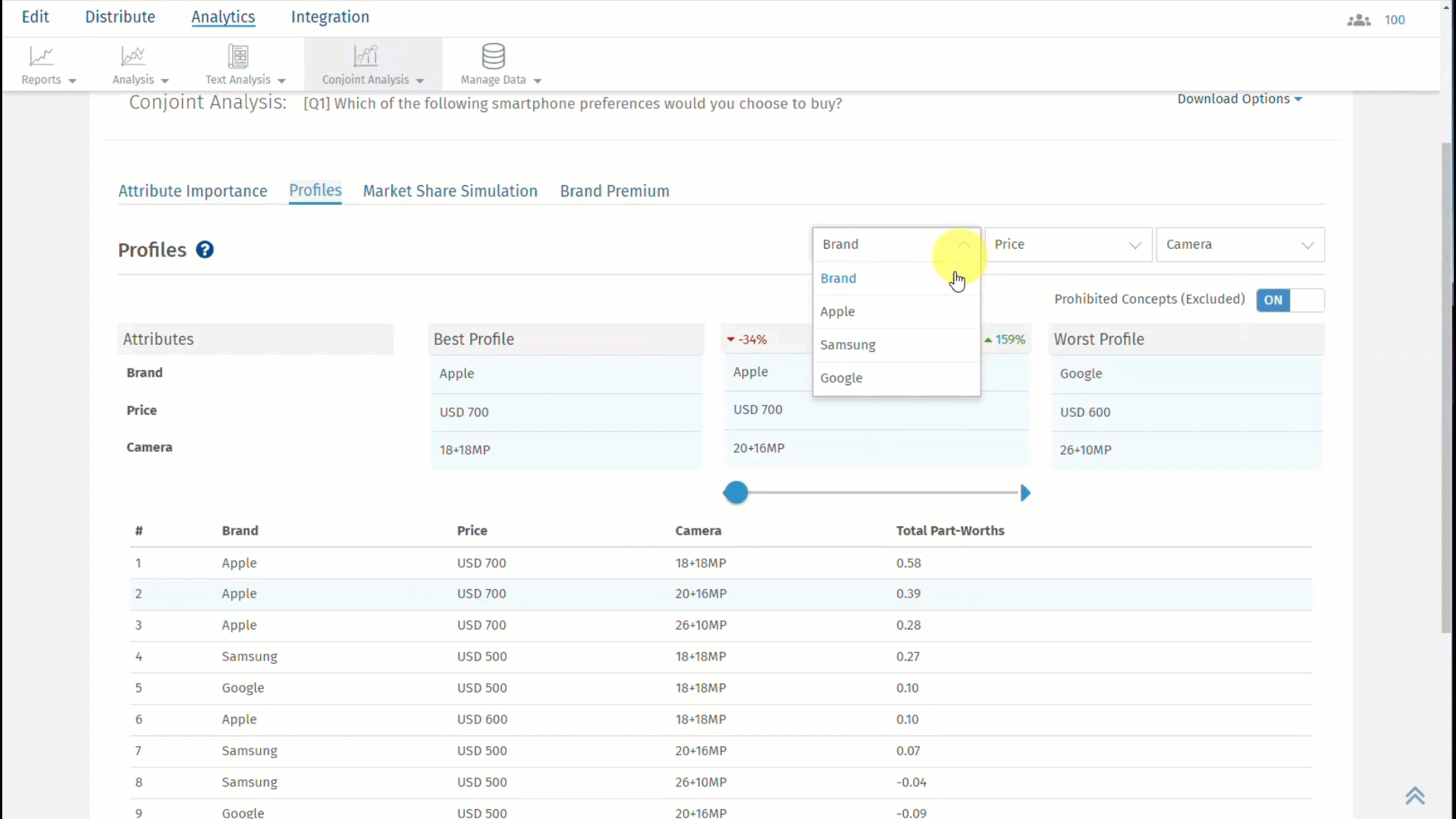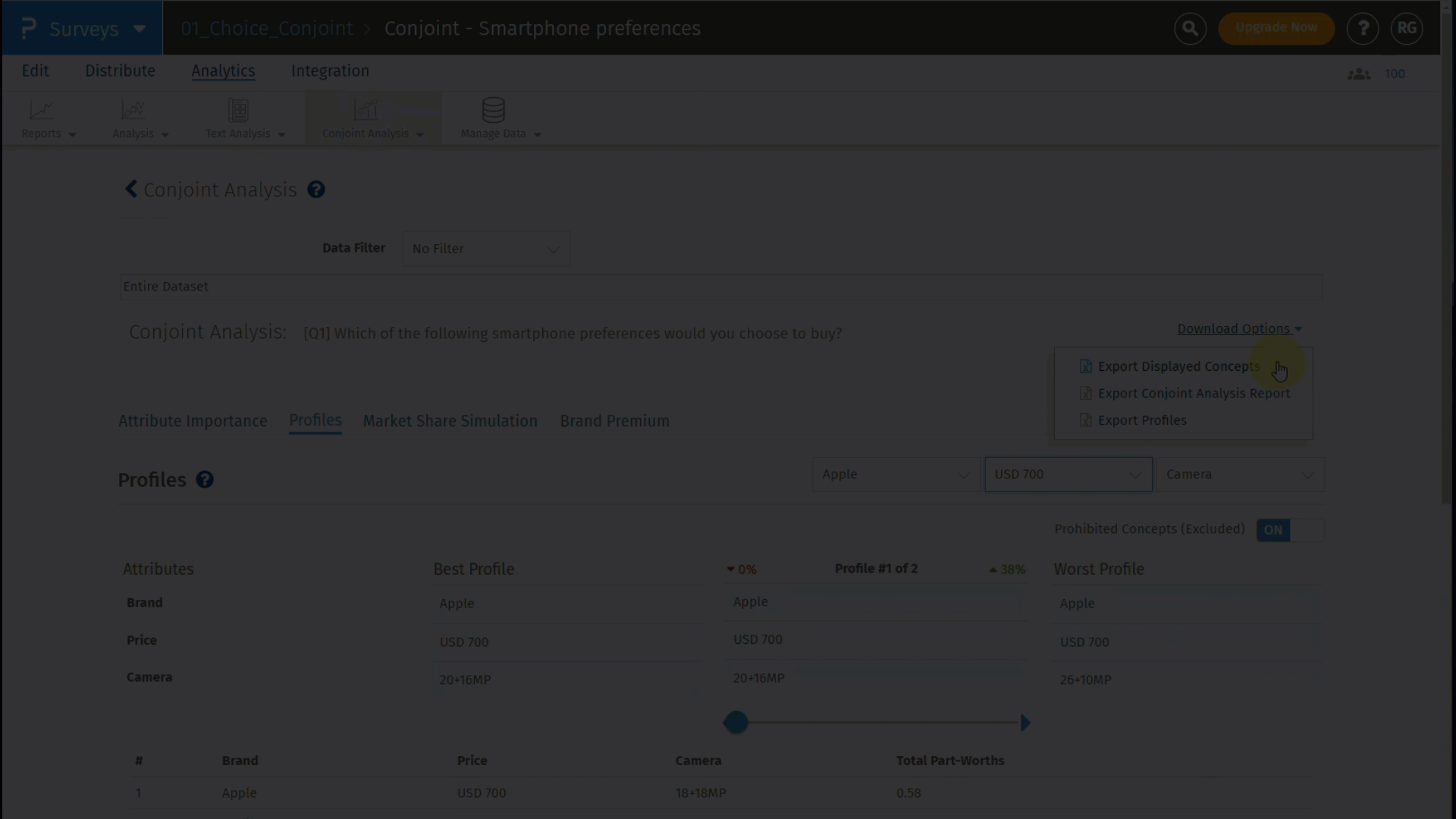

Click to download video

Click on Analytics

Go To: Choice Modelling » Conjoint Analysis

Select the question for which analysis is required and click on Next Step

Click on the second tab, which is, Profiles and results will be displayed as shown below:

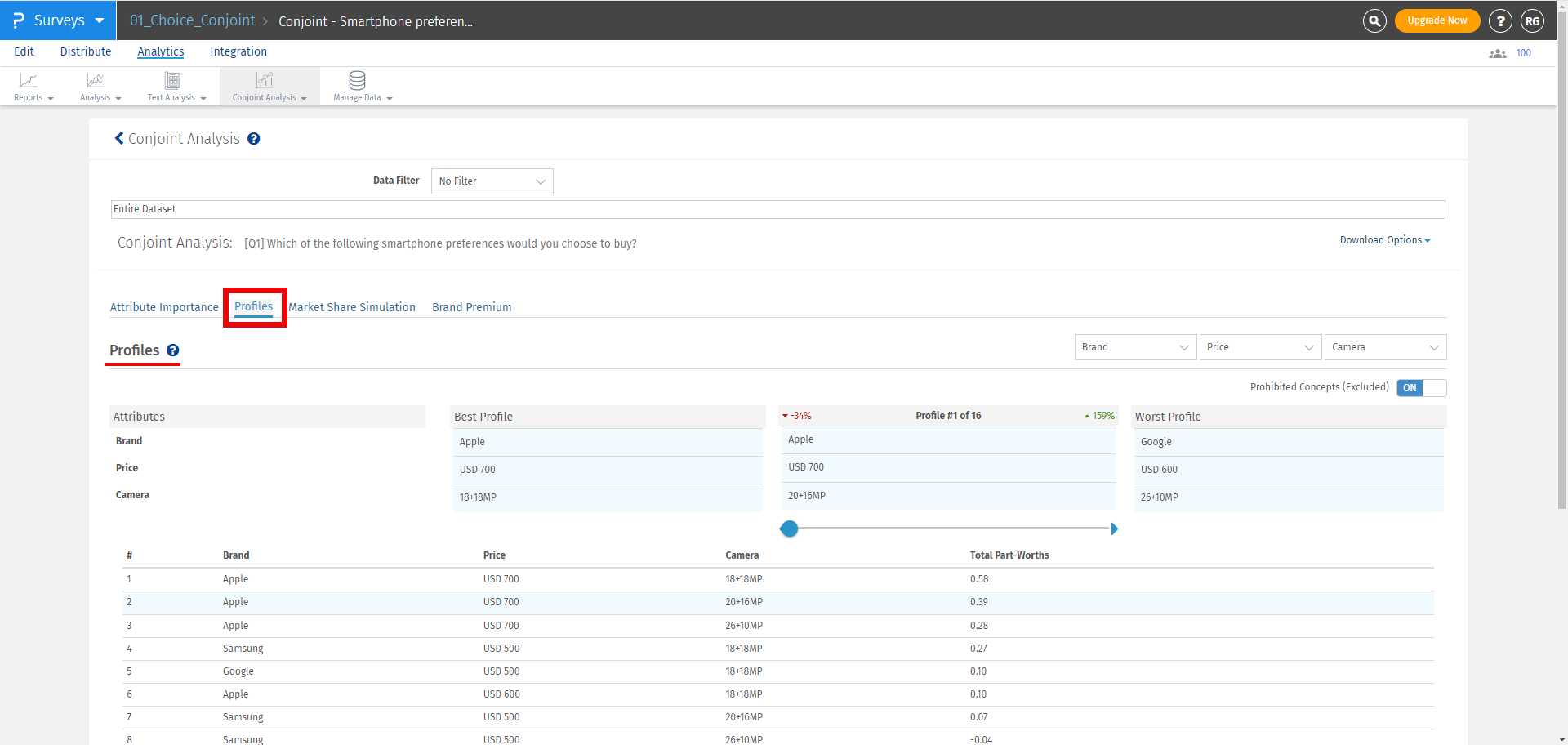The best profile is always displayed on the left and the worst profile on the right. In between, you can select a custom profile to see how it compares with the best and the worst profile.

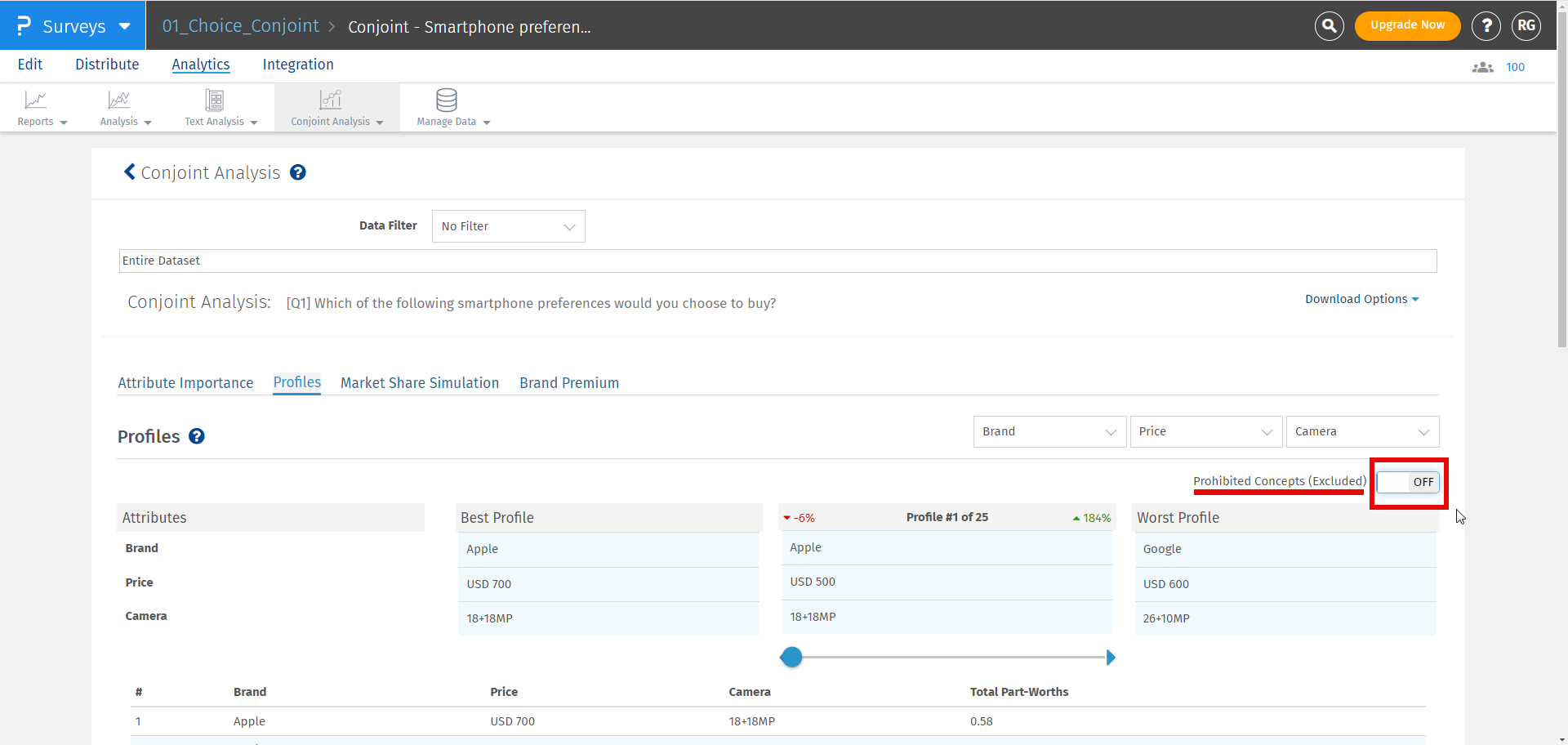
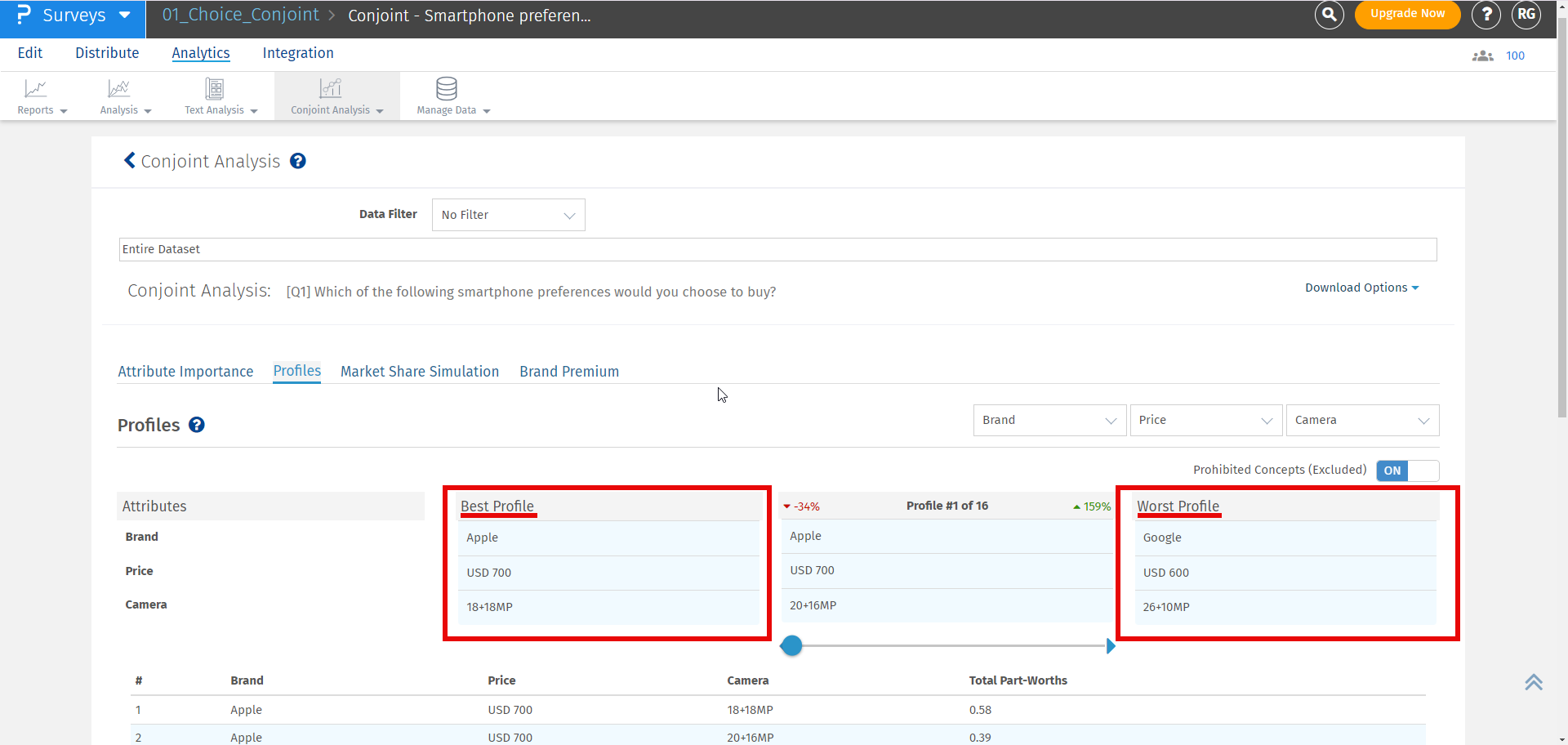If any pair is selected in prohibited pair that will not be displayed in best, worst or custom profile.If user still want to see the prohibited pairs they can enable the including prohibited pairs option provided

For the selected profile, you can see the percentage point difference between the best profile and the selected profile in red. On the other hand, the percentage point difference between the worst profile and the selected profile is displayed in green.

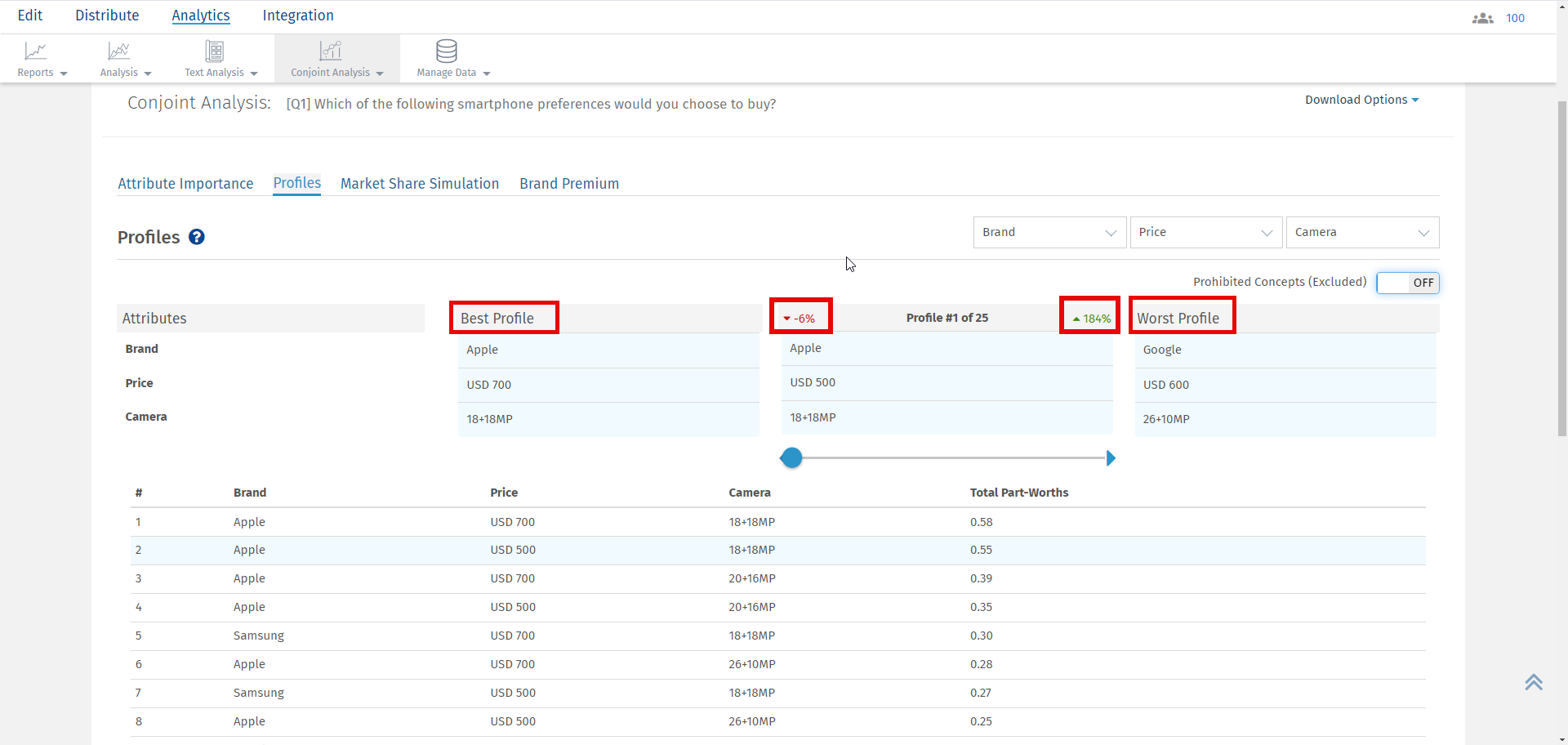Note: Attribute and level with highest Total Part Worth Value will be selected as the Best Profile and the one with lowest Total Part Worth value will be selected as the Worst Profile

We use the following algorithm to calculate CBC Conjoint Part-Worths:

Notation

Let there be R respondents, with individuals r = 1 ... R

Let each respondent see T tasks, with t = 1 ... T

Let each task t have C configurations (or concepts), with c = 1 ... C (C in our case is usually 3 or 4)

If we have A attributes, a = 1 to A, with each attribute having La levels, l = 1 to La, then the part-worth for a particular attribute/level is w’(a,l). It is this (jagged array) of part worths we are solving for in this exercise.

We can simplify this to a one-dimensional array w(s), where the elements are:{w’(1,1), w’(1,2) ... w’(1,L1), w’(2,1) ... w’(A,LA)} with w having S elements.

A specific configuration x can be represented as a one-dimensional array x(s), where x(s)=1 if the specific level/attribute is present, and 0 otherwise.

Let Xrtc represent the specific configuration of the cth configuration in the tth task for the rth respondent. Thus the experiment design is represented by the four dimensional matrix X with size RxTxCxS

If respondent r chooses configuration c in task t then let Yrtc=1; otherwise 0.

Utility Of A Specific Configuration

The Utility Ux of a specific configuration is the sum of the part-worths for those attribute/levels present in the configuration, i.e. it is the scalar product x.w

The Multinomial Logit Model

For a simple choice between two configurations, with utilities U1 and U2, the MNL model predicts that configuration 1 will be chosen

EXP(U1)/(EXP(U1) + EXP(U2)) of the time (a number between 0 and 1).

For a choice between N configurations, configuration 1 will be chosen

EXP(U1)/(EXP(U1) + EXP(U2) + ... + EXP(UN)) of the time.

Modeled Choice Probability

Let the choice probability (using MNL model) of choosing the cth configuration in the tth task for the rth respondent be:

Prtc=EXP(xrtc.w)/SUM(EXP(xrt1.w), EXP(xrt2.w), ... , EXP(xrtC.w))

Log-likelihood Measure

The Log-Likelihood measure LL is calculated as:

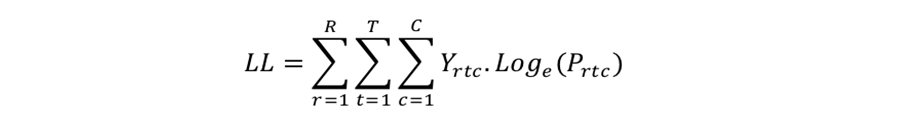
Prtc is a function of the part-worth vector w, which is the set of part-worths we are solving for.

Solving For Part-worths Using Maximum Likelihood

We solve for the part-worth vector by finding the vector w that gives the maximum value for LL. Note that we are solving for S variables.

This is a multi-dimensional non-linear continuous maximization problem, and requires a standard solver library. We use the Nelder-Mead Simplex Algorithm.

The Log-Likelihood function should be implemented as a function LL(w, Y, X), and then optimized to find the vector w that gives us a maximum. The responses Y, and the design X are given, and constant for a specific optimization. Initial values for w can be set to the origin 0.

The final part-worths w are re-scaled so that the part-worths for any attribute have a mean of zero, simply by subtracting the mean of the part-worths for all levels of each attribute.